
【题目】对于函数![]() ,若存在定义域中的实数
,若存在定义域中的实数![]() ,
,![]() 满足
满足![]() 且
且![]() ,则称函数
,则称函数![]() 为“
为“![]() 类” 函数.
类” 函数.
(1)试判断![]() ,
,![]() 是否是“
是否是“![]() 类” 函数,并说明理由;
类” 函数,并说明理由;
(2)若函数![]() ,
,![]() ,
,![]() 为“
为“![]() 类” 函数,求
类” 函数,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】某种体育比赛的规则是:进攻队员与防守队员均在安全线![]() 的垂线
的垂线![]() 上(
上(![]() 为垂足),且分别位于距
为垂足),且分别位于距![]() 为
为![]() 和
和![]() 的点
的点![]() 和点
和点![]() 处,进攻队员沿直线
处,进攻队员沿直线![]() 向安全线跑动,防守队员沿直线方向拦截,设
向安全线跑动,防守队员沿直线方向拦截,设![]() 和
和![]() 交于点
交于点![]() ,若在
,若在![]() 点,防守队员比进攻队员先到或同时到,则进攻队员失败,已知进攻队员速度是防守队员速度的两倍,且他们双方速度不变,问进攻队员的路线
点,防守队员比进攻队员先到或同时到,则进攻队员失败,已知进攻队员速度是防守队员速度的两倍,且他们双方速度不变,问进攻队员的路线![]() 应为什么方向才能取胜?
应为什么方向才能取胜?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() ,直线l过点
,直线l过点![]() .
.

(1)若直线l与圆心C的距离为1,求直线l的方程;
(2)若直线l与圆C交于M,N两点,且![]() ,求以MN为直径的圆的方程;
,求以MN为直径的圆的方程;
(3)设直线![]() 与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网技术的快速发展,人们更加关注如何高效地获取有价值的信息,网络知识付费近两年呈现出爆发式的增长,为了了解网民对网络知识付费的态度,某网站随机抽查了![]() 岁及以上不足
岁及以上不足![]() 岁的网民共
岁的网民共![]() 人,调查结果如下:
人,调查结果如下:

(1)请完成上面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下,能否认为网民对网络知识付费的态度与年龄有关?
的前提下,能否认为网民对网络知识付费的态度与年龄有关?
(2)在上述样本中用分层抽样的方法,从支持和反对网络知识付费的两组网民中抽取![]() 名,若在上述
名,若在上述![]() 名网民中随机选
名网民中随机选![]() 人,求至少1人支持网络知识付费的概率.
人,求至少1人支持网络知识付费的概率.
附:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数x,满足
,若在定义域内存在实数x,满足![]() ,其中k为整数,则称函数
,其中k为整数,则称函数![]() 为定义域上的“k阶局部奇函数”.
为定义域上的“k阶局部奇函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为
是否为![]() 上的“2阶局部奇函数”?并说明理由;
上的“2阶局部奇函数”?并说明理由;
(2)若![]() 是
是![]() 上的“1阶局部奇函数”,求实数m的取值范围;
上的“1阶局部奇函数”,求实数m的取值范围;
(3)若![]() ,对任意的实数
,对任意的实数![]() ,函数
,函数![]() 恒为
恒为![]() 上的“k阶局部奇函数”,求整数k取值的集合.
上的“k阶局部奇函数”,求整数k取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
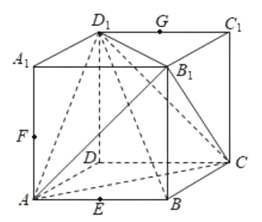
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+6|﹣|m﹣x|(m∈R)
(1)当m=3时,求不等式f(x)≥5的解集;
(2)若不等式f(x)≤7对任意实数x恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com