
【题目】已知![]() 为实常数,函数
为实常数,函数![]() .
.
(1)若![]() 在
在![]() 是减函数,求实数
是减函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时函数
时函数![]() 有两个不同的零点
有两个不同的零点![]() ,求证:
,求证:![]() 且
且![]() .(注:
.(注:![]() 为自然对数的底数);
为自然对数的底数);
(3)证明![]()
【答案】(1)![]() (2)见解析
(2)见解析
【解析】分析:(1) 因![]() ,则
,则![]() ,又
,又![]() 在
在![]() 是减函数所以
是减函数所以![]() 在
在![]() 时恒成立,则实数
时恒成立,则实数![]() 的取值范围为
的取值范围为![]() ;(2)先证明下当
;(2)先证明下当![]() 时,
时,![]() ,由(1)知
,由(1)知![]() ,则
,则![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,由
内单调递减,由![]() ,得
,得![]() .所以
.所以![]() ,
,![]() ;(3)由(1)知当
;(3)由(1)知当![]() 时,
时,![]() ,当
,当![]() 时,有
时,有![]() ,即
,即![]() ,累加可得结果.
,累加可得结果.
详解:(1)因![]() ,则
,则![]() ,又
,又![]() 在
在![]() 是减函数所以
是减函数所以![]() 在
在![]() 时恒成立,则实数
时恒成立,则实数![]() 的取值范围为
的取值范围为![]()
(2)因当![]() 时函数
时函数![]() 有两个不同的零点
有两个不同的零点![]() ,则有
,则有![]() ,
,
则有![]() .设
.设![]() .
. ![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.![]() 最大值为
最大值为![]() .
.
由于![]() ,且
,且![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
下面证明:当![]() 时,
时,![]() .设
.设![]() ,
,
则![]() .
.![]() 在
在![]() 上是增函数,
上是增函数,
所以当![]() 时,
时,![]() .即当
.即当![]() 时,
时,![]() ..
..
由![]() 得
得![]() .所以
.所以![]() .
.
所以![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() .而
.而![]() ,则有
,则有![]() .
.
由(1)知![]() ,则
,则![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,
由![]() ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
(3)由(1)知当![]() 时,
时,![]() 在
在![]() 上是减函数,且
上是减函数,且![]()
所以当![]() 时恒有
时恒有![]() ,即
,即![]()
当![]() 时,有
时,有![]() ,即
,即![]() ,
,
累加得:![]() (
(![]() )
)


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
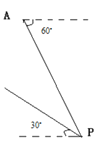
【题目】据监测,在海滨某城市附近的海面有一台风. 台风中心位于城市![]() 的东偏南
的东偏南![]() 方向、距离城市
方向、距离城市![]() 的海面
的海面![]() 处,并以
处,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移动(如图示).如果台风侵袭范围为圆形区域,半径
方向移动(如图示).如果台风侵袭范围为圆形区域,半径![]() ,台风移动的方向与速度不变,那么该城市受台风侵袭的时长为_____ .
,台风移动的方向与速度不变,那么该城市受台风侵袭的时长为_____ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,AD=1,CD=2,AC= ![]() .
. 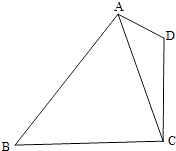
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高级中学共有学生2000名,各年级男、女生人数如下表:
高一年级 | 高二年级 | 高三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应该在高三年级抽取多少名?
(3)已知![]() ,
,![]() ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象过点
的一段图象过点![]() ,如图所示.
,如图所示.
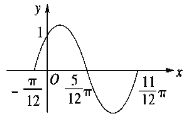
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求
的图象,求![]() 的最大值,并求出此时自变量
的最大值,并求出此时自变量![]() 的集合,并写出该函数的增区间.
的集合,并写出该函数的增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题的序号为__________.
①已知随机变量服从二项分布![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() ;
;
④某人在![]() 次射击中,击中目标的次数为
次射击中,击中目标的次数为![]() ,
,![]() ,则当
,则当![]() 时概率最大.
时概率最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年北京国际数学家大会会标,是以中国古代数学家赵爽的弦图为基础而设计的,弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形![]() 如图
如图![]() ,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为
,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为![]() ,则
,则![]() 等于
等于![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com