
【题目】数学中的数形结合也可以组成世间万物的绚丽画面,一些优美的曲线是数学形象美、对称美、和谐美的产物,曲线![]() 为四叶玫瑰线,下列结论正确的有( )
为四叶玫瑰线,下列结论正确的有( )
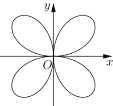
(1)方程![]() (
(![]() ),表示的曲线在第二和第四象限;
),表示的曲线在第二和第四象限;
(2)曲线![]() 上任一点到坐标原点
上任一点到坐标原点![]() 的距离都不超过2;
的距离都不超过2;
(3)曲线![]() 构成的四叶玫瑰线面积大于
构成的四叶玫瑰线面积大于![]() ;
;
(4)曲线![]() 上有5个整点(横、纵坐标均为整数的点);
上有5个整点(横、纵坐标均为整数的点);
A.(1)(2)B.(1)(2)(3)
C.(1)(2)(4)D.(1)(3)(4)
【答案】A
【解析】
因为![]() ,所以
,所以![]() 与
与![]() 异号,仅限与第二和四象限,从而判断(1).
异号,仅限与第二和四象限,从而判断(1).
利用基本不等式![]() 即可判断(2);
即可判断(2);
将以![]() 为圆心、2为半径的圆的面积与曲线
为圆心、2为半径的圆的面积与曲线![]() 围成区域的面积进行比较即可判断(3);
围成区域的面积进行比较即可判断(3);
先确定曲线![]() 经过点
经过点![]() ,再将
,再将![]() ,
,![]() 的整点
的整点![]() ,
,![]() 和
和![]() 逐一代入曲线
逐一代入曲线![]() 的方程进行检验即可判断(4);
的方程进行检验即可判断(4);
对于(1),因为![]() ,所以
,所以![]() 与
与![]() 异号,仅限与第二和四象限,即(1)正确.
异号,仅限与第二和四象限,即(1)正确.
对于(2),因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ,即(2)正确;
,即(2)正确;
对于(3),以![]() 为圆点,2为半径的圆
为圆点,2为半径的圆![]() 的面积为
的面积为![]() ,显然曲线
,显然曲线![]() 围成的区域的面积小于圆
围成的区域的面积小于圆![]() 的面积,即(3)错误;
的面积,即(3)错误;
对于(4),只需要考虑曲线在第一象限内经过的整点即可,把![]() ,
,![]() 和
和![]() 代入曲线
代入曲线![]() 的方程验证可知,等号不成立,所以曲线
的方程验证可知,等号不成立,所以曲线![]() 在第一象限内不经过任何整点,再结合曲线的对称性可知,曲线
在第一象限内不经过任何整点,再结合曲线的对称性可知,曲线![]() 只经过整点
只经过整点![]() ,即(4)错误;
,即(4)错误;
故选:A.


 新课标同步训练系列答案
新课标同步训练系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,
的左,右焦点,![]() 两点分别是椭圆
两点分别是椭圆![]() 的上,下顶点,
的上,下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直
与直![]() 分别相交于
分别相交于![]() 两点,点
两点,点![]() ,求证:
,求证:![]() 的外接圆恒过原点
的外接圆恒过原点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
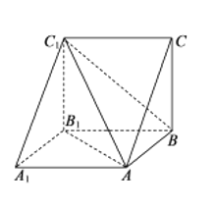
【题目】《九章算术》中记载:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱剖开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵![]() 中,
中,![]() 且有鳖臑C1-ABB1和鳖臑
且有鳖臑C1-ABB1和鳖臑![]() ,现将鳖臑
,现将鳖臑![]() 沿线BC1翻折,使点C与点B1重合,则鳖臑
沿线BC1翻折,使点C与点B1重合,则鳖臑![]() 经翻折后,与鳖臑
经翻折后,与鳖臑![]() 拼接成的几何体的外接球的表面积是______.
拼接成的几何体的外接球的表面积是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,用
为实数,用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() ,对于函数
,对于函数![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 是“
是“![]() 函数”.
函数”.
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)设函数![]() 是定义在
是定义在![]() 上的周期函数,其最小正周期是
上的周期函数,其最小正周期是![]() ,若
,若![]() 不是“
不是“![]() 函数”,求
函数”,求![]() 的最小值;
的最小值;
(3)若函数![]() 是“
是“![]() 函数”,求
函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为1.
截得的弦长为1.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 两点,与线段
两点,与线段![]() 和椭圆短轴分别交于两个不同点
和椭圆短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为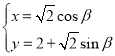 (
(![]() 为参数),直线
为参数),直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)若相交于不同的两点![]() ,求
,求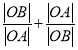 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com