
【题目】对数是简化繁杂运算的产物.16世纪时,为了简化数值计算,数学家希望将乘除法归结为简单的加减法.当时已经有数学家发现这在某些情况下是可以实现的.
比如,利用以下2的次幂的对应表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16与256;然后找出它们在第一行对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4096,这就是![]() 的值.
的值.
用类似的方法可以算出![]() 的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是
的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是![]() 值.
值.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度,在2060岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如图所示:
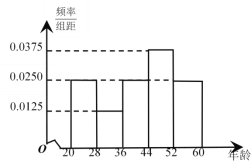
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会,现从这8人中随机抽2人.记抽到44岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: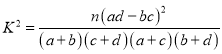 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对一切正整数
,且对一切正整数![]() 都有
都有![]() .
.
(1)求证:![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在实数![]() ,使不等式
,使不等式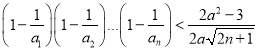 ,对一切正整数
,对一切正整数![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() 经过椭圆
经过椭圆![]() 的左右焦点
的左右焦点![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
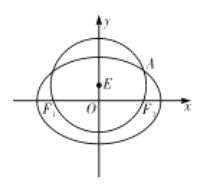
(1)求椭圆![]() 的方程;
的方程;
(2)设与直线![]() (
(![]() 为原点)平行的直线交椭圆
为原点)平行的直线交椭圆![]() 于
于![]() 两点,当
两点,当![]() 的面积取取最大值时,求直线
的面积取取最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和圆
和圆![]() ,
,![]() 、
、![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(I)求![]() 的方程;
的方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民用天然气实行阶梯价格制度,具体见下表:
阶梯 | 年用气量(立方米) | 价格(元/立方米) |
第一阶梯 | 不超过228的部分 | 3.25 |
第二阶梯 | 超过228而不超过348的部分 | 3.83 |
第三阶梯 | 超过348的部分 | 4.70 |
从该市随机抽取10户(一套住宅为一户)同一年的天然气使用情况,得到统计表如下:
居民用气编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年用气量(立方米) | 95 | 106 | 112 | 161 | 210 | 227 | 256 | 313 | 325 | 457 |
(1)求一户居民年用气费y(元)关于年用气量x(立方米)的函数关系式;
(2)现要在这10户家庭中任意抽取3户,求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望;
(3)若以表中抽到的10户作为样本估计全市居民的年用气情况,现从全市中依次抽取10户,其中恰有k户年用气量不超过228立方米的概率为![]() ,求
,求![]() 取最大值时的值.
取最大值时的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com