
【题目】某市居民用天然气实行阶梯价格制度,具体见下表:
阶梯 | 年用气量(立方米) | 价格(元/立方米) |
第一阶梯 | 不超过228的部分 | 3.25 |
第二阶梯 | 超过228而不超过348的部分 | 3.83 |
第三阶梯 | 超过348的部分 | 4.70 |
从该市随机抽取10户(一套住宅为一户)同一年的天然气使用情况,得到统计表如下:
居民用气编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年用气量(立方米) | 95 | 106 | 112 | 161 | 210 | 227 | 256 | 313 | 325 | 457 |
(1)求一户居民年用气费y(元)关于年用气量x(立方米)的函数关系式;
(2)现要在这10户家庭中任意抽取3户,求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望;
(3)若以表中抽到的10户作为样本估计全市居民的年用气情况,现从全市中依次抽取10户,其中恰有k户年用气量不超过228立方米的概率为![]() ,求
,求![]() 取最大值时的值.
取最大值时的值.
【答案】(1)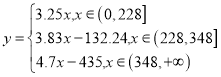 ;(2)分布列见解析,数学期望为
;(2)分布列见解析,数学期望为![]() ;(3)6.
;(3)6.
【解析】
(1)由表格中的数据结合题意,即可求得一户居民年用气费y(元)关于年用气量x(立方米)的函数关系式;
(2)由题意知10户家庭中年用气量超过228立方米而不超过348立方米的用户有3户,得到随机变量![]() 可取
可取![]() ,利用超几何分布求得相应的概率,得到随机变量的分布列,进而求得期望;
,利用超几何分布求得相应的概率,得到随机变量的分布列,进而求得期望;
(3)由![]() ,列出不等式组由
,列出不等式组由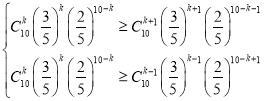 ,求得
,求得![]() 的值,即可求解.
的值,即可求解.
(1)由题意,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以年用气费y关于年用气量x的函数关系式为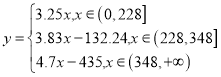 .
.
(2)由题知10户家庭中年用气量超过228立方米而不超过348立方米的用户有3户,
设取到年用气量超过228立方米而不超过348立方米的用户数为![]() ,则
,则![]() 可取
可取![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
故随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以![]() .
.
(3)由题意知![]() ,
,
由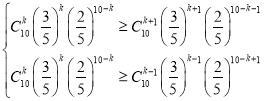 ,解得
,解得![]() ,
,![]() ,
,
所以当![]() 时,概率
时,概率![]() 最大,所以
最大,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】对数是简化繁杂运算的产物.16世纪时,为了简化数值计算,数学家希望将乘除法归结为简单的加减法.当时已经有数学家发现这在某些情况下是可以实现的.
比如,利用以下2的次幂的对应表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16与256;然后找出它们在第一行对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4096,这就是![]() 的值.
的值.
用类似的方法可以算出![]() 的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是
的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: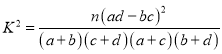 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
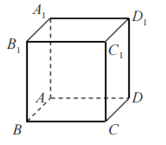
【题目】在如图所示的棱长为1的正方体![]() 中,点P在侧面
中,点P在侧面![]() 所在的平面上运动,则下列命题中正确的( )
所在的平面上运动,则下列命题中正确的( )
A.若点P总满足![]() ,则动点P的轨迹是一条直线
,则动点P的轨迹是一条直线
B.若点P到点A的距离为![]() ,则动点P的轨迹是一个周长为
,则动点P的轨迹是一个周长为![]() 的圆
的圆
C.若点P到直线AB的距离与到点C的距离之和为1,则动点P的轨迹是椭圆
D.若点P到直线AD与直线![]() 的距离相等,则动点P的轨迹是双曲线
的距离相等,则动点P的轨迹是双曲线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为某大学环境科学专业,按照该大学上一年高考招生选考科目要求理、化必选,为该生安排课表(上午四节、下午四节,每门课每天至少一节),已知该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻(上午第四节和下午第一节不算相邻),则该生该天课表有( ).
A.444种B.1776种C.1440种D.1560种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市开发了一块等腰梯形的菜花风景区![]() (如图).经测量,
(如图).经测量,![]() 长为
长为![]() 百米,
百米,![]() 长为
长为![]() 百米,
百米,![]() 与
与![]() 相距
相距![]() 百米,田地内有一条笔直的小路
百米,田地内有一条笔直的小路![]() (
(![]() 在
在![]() 上,
上,![]() 在
在![]() 上)与
上)与![]() 平行且相距
平行且相距![]() 百米.现准备从风景区入口处
百米.现准备从风景区入口处![]() 出发再修一条笔直的小路
出发再修一条笔直的小路![]() 与
与![]() 交于
交于![]() ,在小路
,在小路![]() 与
与![]() 的交点
的交点![]() 处拟建一座瞭望塔.
处拟建一座瞭望塔.
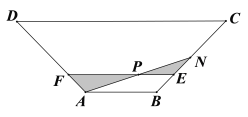
(1)若瞭望塔![]() 恰好建在小路
恰好建在小路![]() 的中点处,求小路
的中点处,求小路![]() 的长;
的长;
(2)两条小路![]() 与
与![]() 将菜花风景区划分为四个区域,若将图中阴影部分规划为观赏区.求观赏区面积
将菜花风景区划分为四个区域,若将图中阴影部分规划为观赏区.求观赏区面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过![]() 轴正半轴上的动点
轴正半轴上的动点![]() 作曲线
作曲线![]() :
:![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,设曲线
,设曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
(1)求![]() 的大小及
的大小及![]() 的轨迹方程;
的轨迹方程;
(2)当动点![]() 到直线
到直线![]() 的距离最小时,求
的距离最小时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为坐标原点,过点
为坐标原点,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() ,
,![]() ,试探究:
,试探究:![]() 是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com