
【题目】如图,在多面体ABCED中,BE⊥CD,平面ABED⊥平面BCE.在梯形ABED中,AB∥DE,BE⊥AB.DE=BE=CE=2AB,M是BC的中点,点N在线段DE上,且满足DN=![]() DE.
DE.

(1)求证:MN∥平面ACD;
(2)若AB=2,求点N到平面ABC的距离.
【答案】(1)见解析;(2)2![]()
【解析】
(1)证法一:设![]() 的中点为
的中点为![]() ,证明
,证明![]() ,从而
,从而![]() ,通过线面平行证明
,通过线面平行证明![]() 平面
平面![]() .
.
证法二:设![]() 的中点为
的中点为![]() ,证明
,证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,通过面面平行,证明
,通过面面平行,证明![]() 平面
平面![]() .
.
(2)通过![]() 得到
得到![]() 平面
平面![]() ,从而
,从而![]() 到平面
到平面![]() 的距离,转化为
的距离,转化为![]() 到平面
到平面![]() 的距离,再证明
的距离,再证明![]() 平面
平面![]() ,在
,在![]() 中,求出
中,求出![]() 的长.
的长.
(1)证法一:设![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
又![]() ,
,![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
证法二:设![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]() 平面
平面![]() .
.
(2)连结![]() ,
,
![]() ,
,![]() 为
为![]() 的中点,
的中点,
![]() ,
,
又![]() ,平面
,平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 为
为![]() 到平面
到平面![]() 的距离,
的距离,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】英语老师要求学生从星期一到星期四每天学习3个英语单词:每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(I)英语老师随机抽了![]() 个单词进行检测,求至少有
个单词进行检测,求至少有![]() 个是后两天学习过的单词的概率;
个是后两天学习过的单词的概率;
(Ⅱ)某学生对后两天所学过的单词每个能默写对的概率为![]() ,对前两天所学过的单词每个能默写对的概率为
,对前两天所学过的单词每个能默写对的概率为![]() ,若老师从后三天所学单词中各抽取一个进行检测,求该学生能默写对的单词的个数
,若老师从后三天所学单词中各抽取一个进行检测,求该学生能默写对的单词的个数![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某艺术团组织的“微视频展示”活动中,该团体将从微视频的“点赞量”和“专家评分”两个角度来进行评优.若A视频的“点赞量”和“专家评分”中至少有一项高于B视频,则称A视频不亚于B视频.已知共有5部微视频展,如果某微视频不亚于其他4部视频,就称此视频为优秀视频.那么在这5部微视频中,最多可能有_______个优秀视频.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式: 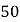 ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: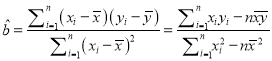 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过定点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,点
,点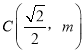 满足
满足![]() .
.
(1)若以原点为圆心的圆![]() 与
与![]() 有唯一公共点,求圆
有唯一公共点,求圆![]() 的轨迹方程;
的轨迹方程;
(2)求能覆盖![]() 的最小圆的面积;
的最小圆的面积;
(3)在(1)的条件下,点![]() 在直线
在直线![]() 上,圆
上,圆![]() 上总存在两个不同的点
上总存在两个不同的点![]() 使得
使得![]()
![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】青岛二中高一高二高三三个年级数学MT的学生人数分别为240人,240人,120人,现采用分层抽样的方法从中抽取5名同学参加团队内部举办的趣味数学比赛,再从5位同学中选出2名一等奖记A=“两名一等奖来自同一年级”,则事件A的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是__________________.
①命题“若x2-3x+2=0,则x=1”的逆否命题为:若x≠1,则x2-3x+2≠0
②x=1是x2-3x+2=0的充分不必要条件
③若p∧q为假命题,则p,q均为假命题
④对于命题p:x∈R,使得x2+x+1<0,则非p:x∈R, 均有x2+x+1≥0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com