
已知向量 =(cos
=(cos x,sin
x,sin x),
x),  ,且x∈[0,
,且x∈[0, ].
].
(1)求
(2)设函数 =
= +
+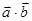 ,求函数
,求函数 的最值及相应的
的最值及相应的 的值。
的值。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知向量 ,函数
,函数 .
.
(1)求 的单调区间;
的单调区间;
(2)请说出 的图象是由
的图象是由 的图象经过怎样的变换得到的(说清每一步的变换方法);
的图象经过怎样的变换得到的(说清每一步的变换方法);
(3)当 时,求
时,求 的最大值及取得最大值时的
的最大值及取得最大值时的 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数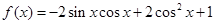
(1)设方程 在(0,
在(0,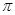 )内有两个零点
)内有两个零点 ,求
,求 的值;
的值;
(2)若把函数 的图像向左移动
的图像向左移动
 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于 轴对称,求
轴对称,求 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据市气象站对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(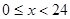 ,单位为小时,
,单位为小时, 表示气温,单位为摄氏度,
表示气温,单位为摄氏度,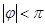 ,
,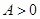 ),
),
现已知这天气温为4至12摄氏度,并得知在凌晨1时整气温最低,下午13时整气温最高。
(1)求这条曲线的函数表达式;
(2)求这一天19时整的气温。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若 =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ·
· ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为 ,
,
(1)求 的值;
的值;
(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com