
【题目】由于近几年我国多地区的雾霾天气,引起口罩热销,某厂家拟在2017年举行促销活动,经调查该批口罩销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为常数).已知生产该批口罩还要投入成本
为常数).已知生产该批口罩还要投入成本![]() 万元(不包含促销费用),口罩的销售价格定为
万元(不包含促销费用),口罩的销售价格定为![]() 元/件.
元/件.
(1)将该批口罩的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)当促销费用投入多少万元时,该厂家的利润最大?
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民区有一个银行网点(以下简称“网点”),网点开设了若干个服务窗口,每个窗口可以办理的业务都相同,每工作日开始办理业务的时间是8点30分,8点30分之前为等待时段.假设每位储户在等待时段到网点等待办理业务的概率都相等,且每位储户是否在该时段到网点相互独立.根据历史数据,统计了各工作日在等待时段到网点等待办理业务的储户人数,得到如图所示的频率分布直方图:
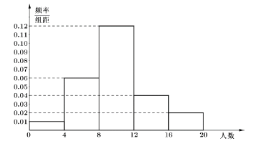
(1)估计每工作日等待时段到网点等待办理业务的储户人数的平均值;
(2)假设网点共有1000名储户,将频率视作概率,若不考虑新增储户的情况,解决以下问题:
①试求每位储户在等待时段到网点等待办理业务的概率;
②储户都是按照进入网点的先后顺序,在等候人数最少的服务窗口排队办理业务.记“每工作日上午8点30分时网点每个服务窗口的排队人数(包括正在办理业务的储户)都不超过3”为事件![]() ,要使事件
,要使事件![]() 的概率不小于0.75,则网点至少需开设多少个服务窗口?
的概率不小于0.75,则网点至少需开设多少个服务窗口?
参考数据:![]() ;
;![]() ;
;
![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019超长“三伏”来袭,虽然大部分人都了解“伏天”不宜吃生冷食物,但随着气温的不断攀升,仍然无法阻挡冷饮品销量的暴增.现在,某知名冷饮品销售公司通过随机抽样的方式,得到其100家加盟超市3天内进货总价的统计结果如下表所示:
组别(单位:百元) |
|
|
|
|
|
|
频数 | 3 | 11 | 20 | 27 | 26 | 13 |
(1)由频数分布表大致可以认为,被抽查超市3天内进货总价![]() ,μ近似为这100家超市3天内进货总价的平均值(同一组中的数据用该组区间的中点值作代表),利用正态分布,求
,μ近似为这100家超市3天内进货总价的平均值(同一组中的数据用该组区间的中点值作代表),利用正态分布,求![]() ;
;
(2)在(1)的条件下,该公司为增加销售额,特别为这100家超市制定如下抽奖方案:
①令m表示“超市3天内进货总价超过μ的百分点”,其中![]() .若
.若![]() ,则该超市获得1次抽奖机会;
,则该超市获得1次抽奖机会;![]() ,则该超市获得2次抽奖机会;
,则该超市获得2次抽奖机会;![]() ,则该超市获得3次抽奖机会;
,则该超市获得3次抽奖机会;![]() ,则该超市获得4次抽奖机会;
,则该超市获得4次抽奖机会;![]() ,则该超市获得5次抽奖机会;
,则该超市获得5次抽奖机会;![]() ,则该超市获得6次抽奖机会.另外,规定3天内进货总价低于μ的超市没有抽奖机会;
,则该超市获得6次抽奖机会.另外,规定3天内进货总价低于μ的超市没有抽奖机会;
②每次抽奖中奖获得的奖金金额为1000元,每次抽奖中奖的概率为![]() .
.
设超市A参加了抽查,且超市A在3天内进货总价![]() 百元.记X(单位:元)表示超市A获得的奖金总额,求X的分布列与数学期望.
百元.记X(单位:元)表示超市A获得的奖金总额,求X的分布列与数学期望.
附参考数据与公式:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() (
(![]() ,
,![]() )的右焦点
)的右焦点![]() ,且椭圆
,且椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() 的面积
的面积![]() .
.
①求证:![]() 为定值;
为定值;
②设直线![]() 的中点
的中点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,合肥一中积极开展美丽校园建设,现拟在边长为0.6千米的正方形地块![]() 上划出一片三角形地块
上划出一片三角形地块![]() 建设小型生态园,点
建设小型生态园,点![]() 分别在边
分别在边![]() 上.
上.
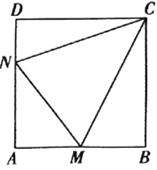
(1)当点![]() 分别时边
分别时边![]() 中点和
中点和![]() 靠近
靠近![]() 的三等分点时,求
的三等分点时,求![]() 的余弦值;
的余弦值;
(2)实地勘察后发现,由于地形等原因,![]() 的周长必须为1.2千米,请研究
的周长必须为1.2千米,请研究![]() 是否为定值,若是,求此定值,若不是,请说明理由.
是否为定值,若是,求此定值,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com