
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() (
(![]() ,
,![]() )的右焦点
)的右焦点![]() ,且椭圆
,且椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() 的面积
的面积![]() .
.
①求证:![]() 为定值;
为定值;
②设直线![]() 的中点
的中点![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①证明见解析;②
(2)①证明见解析;②![]() .
.
【解析】
(1)由题意可得![]() ,
,![]() ,求得
,求得![]() 后即可得解;
后即可得解;
(2)①当直线斜率不存在时易得![]() ,当直线斜率存在时,设直线方程为
,当直线斜率存在时,设直线方程为![]() ,可得
,可得![]() 、
、![]() 、
、![]() 、
、![]() ,由
,由![]() 可得
可得![]() ,再利用
,再利用![]() 化简即可得证;
化简即可得证;
②当直线的斜率不存在时,易得![]() ;当直线斜率存在时,设直线方程为
;当直线斜率存在时,设直线方程为![]() ,表示出
,表示出![]() 、
、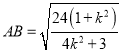 后,再利用基本不等式
后,再利用基本不等式![]() 化简即可得解.
化简即可得解.
(1)![]() 椭圆右焦点为
椭圆右焦点为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() .
.
(2)①证明:当直线![]() 斜率不存在时,设直线方程为
斜率不存在时,设直线方程为![]() ,则
,则![]() ,
,![]() ,
,
易知![]() ,
,![]()
![]() ,
,![]()
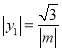 ,
,
![]()
![]() 解得
解得![]() ,此时
,此时![]() .
.
当直线![]() 斜率存在时,设直线方程为
斜率存在时,设直线方程为![]() ,
,
联立方程得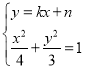 ,消去
,消去![]() 得
得![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
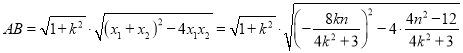
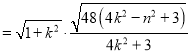 ,
,
又 原点![]() 到直线
到直线![]() 的距离
的距离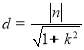 ,
,
![]()
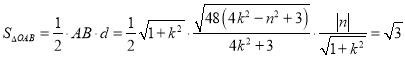 ,
,
化简得![]() ,解得
,解得![]() ,
,
![]()
![]()
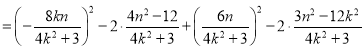
![]() .
.
综上,![]() 为定值7.
为定值7.
②当直线的斜率不存在时,由①知![]() ,
,![]() ,
,
此时![]() ;
;
当直线![]() 斜率存在时,设直线方程为
斜率存在时,设直线方程为![]() ,由①知
,由①知![]() ,
,
![]() ,
,![]() ,
,
![]()
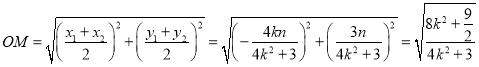 ,
,
即![]() ,
,
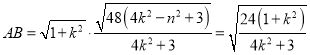 ,
,
![]()
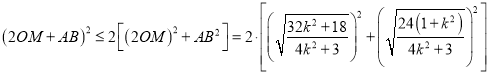
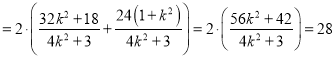 ,
,
当且仅当![]() 即
即![]() 时等号成立,
时等号成立,
![]() 当直线斜率存在时,
当直线斜率存在时,![]() .
.
又![]() ,
,
![]()
![]() 的最大值为
的最大值为![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() .
.
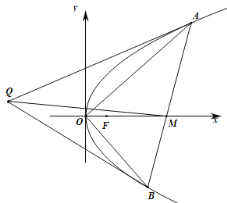
(1)求证:![]() ;
;
(2)求点![]() 的横坐标;
的横坐标;
(3)过![]() 点分别作抛物线的切线,两条切线交于点
点分别作抛物线的切线,两条切线交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某养殖场需要通过某装置对养殖车间进行恒温控制,为了解日用电量![]() 与日平均气温
与日平均气温![]() (℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
(℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
日平均气温(℃) | 3 | 4 | 5 | 6 | 7 |
日用电量( | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)请利用(Ⅰ)中的线性回归方程预测日平均气温为12℃时的日用电量.
附:回归直线的斜率和截距的最小二乘法估计公式分别为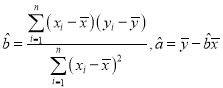 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() 的右准线方程为x=4,右顶点为A,上顶点为B,右焦点为F,斜率为2的直线l经过点A,且点F到直线l的距离为
的右准线方程为x=4,右顶点为A,上顶点为B,右焦点为F,斜率为2的直线l经过点A,且点F到直线l的距离为![]() .
.
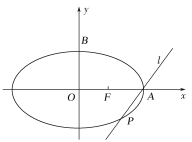
(1)求椭圆C的标准方程.
(2)将直线l绕点A旋转,它与椭圆C相交于另一点P,当B,F,P三点共线时,试确定直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于近几年我国多地区的雾霾天气,引起口罩热销,某厂家拟在2017年举行促销活动,经调查该批口罩销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为常数).已知生产该批口罩还要投入成本
为常数).已知生产该批口罩还要投入成本![]() 万元(不包含促销费用),口罩的销售价格定为
万元(不包含促销费用),口罩的销售价格定为![]() 元/件.
元/件.
(1)将该批口罩的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)当促销费用投入多少万元时,该厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且满足![]() (k∈R).
(k∈R).
(1)求k和数列{an}的通项公式;
(2)若数列{bn}满足bn=![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这个x个分店的年收入之和.

(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程![]()
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式:![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,AD![]() BC,BC⊥CD,BC=CD=2AD=2,PD=
BC,BC⊥CD,BC=CD=2AD=2,PD=![]() ,侧面PBC是等边三角形.
,侧面PBC是等边三角形.
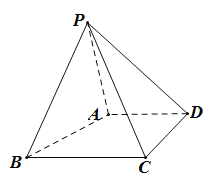
(1)证明:PA⊥平面PBC;
(2)求BC与平面PCD所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com