
【题目】椭圆![]() 的右焦点为
的右焦点为![]() ,左顶点为
,左顶点为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,圆
,圆![]() 过点
过点![]() ,且与
,且与![]() 交于
交于![]() ,
, ![]() 是等腰直角三角形,则圆
是等腰直角三角形,则圆![]() 的标准方程是____________
的标准方程是____________
【答案】![]()
【解析】
设A(﹣a,0),求得AF的中点B的坐标,可得圆F的半径和方程,设D(m,n),(m>0,n>0),E(m,﹣n),由△BDE为等腰直角三角形,可得m,n的关系,将D的坐标代入圆的方程,解方程可得m=1,求出n,代入椭圆方程,解方程可得a=2,即可得到圆F的方程.
如图设A(﹣a,0),可得a>1,c=1,b2=a2﹣1,
线段AF的中点为B(![]() ,0),
,0),
圆F的圆心为F(1,0),半径r=|BF|![]() ,
,
设D(m,n),(m>0,n>0),E(m,﹣n),
由△BDE为等腰直角三角形,可得kBD=1,
即![]() 1,即n=m
1,即n=m![]() ,
,
由D在圆F:(x﹣1)2+y2=(![]() )2上,
)2上,
可得(m﹣1)2+(m![]() )2=(
)2=(![]() )2,
)2,
化简可得(m﹣1)(2m﹣1+a)=0,
解得m=1或m![]() (舍去),
(舍去),
则n![]() ,
,
将D(1,![]() )代入椭圆方程,可得
)代入椭圆方程,可得
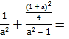 1,
1,
化简可得a=2或![]() (舍去),
(舍去),
则圆F的标准方程为(x﹣1)2+y2![]() ,
,
故答案为:(x﹣1)2+y2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着经济的发展,轿车已成为人们上班代步的一种重要工具.现将某人三年以来每周开车从家到公司的时间之和统计如图所示.
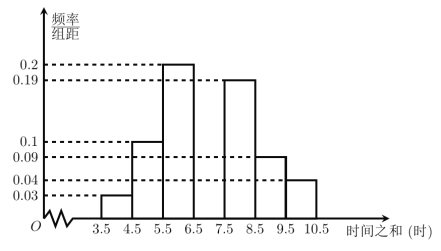
(1)求此人这三年以来每周开车从家到公司的时间之和在![]() (时)内的频率;
(时)内的频率;
(2)求此人这三年以来每周开车从家到公司的时间之和的平均数(每组取该组的中间值作代表);
(3)以频率估计概率,记此人在接下来的四周内每周开车从家到公司的时间之和在![]() (时)内的周数为
(时)内的周数为![]() ,求
,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告明确指出要坚决打赢脱贫攻坚战,让贫困人口和贫困地区同全国一道进入全面小康社会,要动员全党全国全社会力量,坚持精准扶贫、精准脱贫,确保到2020年我国现行标准下农村贫困人口实现脱贫.现有扶贫工作组到某山区贫困村实施脱贫工作.经摸底排查,该村现有贫困农户100户,他们均从事水果种植,2017年底该村平均每户年纯收入为1万元,扶贫工作组一方面请有关专家对水果进行品种改良,提高产量;另一方面,抽出部分农户从事水果包装、销售工作,其户数必须小于种植的户数.从2018年初开始,若该村抽出![]() 户(
户(![]() ,
,![]() )从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高
)从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高![]() ,而从事包装销售农户的年纯收入每户平均为
,而从事包装销售农户的年纯收入每户平均为![]() 万元.(参考数据:
万元.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
(1)至2018年底,该村每户年均纯收入能否达到1.32万元?若能,请求出从事包装、销售的户数;若不能,请说明理由;
(2)至2020年底,为使从事水果种植农户能实现脱贫(即每户(水果种植农户)年均纯收入不低于1.6万元),至少要抽出多少户从事包装、销售工作?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数. 设
为自然对数的底数. 设![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)若![]() 时,函数
时,函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的单调区间;
上的单调区间;
(Ⅲ)若![]() ,函数
,函数![]() 在区间
在区间![]() 内有零点,求
内有零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,且直线
,且直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com