
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数. 设
为自然对数的底数. 设![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)若![]() 时,函数
时,函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的单调区间;
上的单调区间;
(Ⅲ)若![]() ,函数
,函数![]() 在区间
在区间![]() 内有零点,求
内有零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)1(Ⅱ)详见解析(Ⅲ)![]()
【解析】
(I)![]() 时,利用导数的几何意义,求得切线斜率
时,利用导数的几何意义,求得切线斜率![]() ,切点坐标
,切点坐标![]() ,即可求解切线的方程,进而求解
,即可求解切线的方程,进而求解![]() 得值;
得值;
(II)求得函数![]() 的导数
的导数![]() ,根据
,根据![]() 在
在![]() 单调递增,转化为
单调递增,转化为![]() ,分类讨论,即可求解函数
,分类讨论,即可求解函数![]() 的单调区间;
的单调区间;
(Ⅲ)由![]() 得:
得:![]() ,得
,得![]() ,由已知,设
,由已知,设![]() 为
为![]() 在区间
在区间![]() 内的一个零点,则由
内的一个零点,则由![]() 可知
可知![]() 在区间
在区间![]() 上至少有三个单调区间,得到
上至少有三个单调区间,得到![]() 在区间
在区间![]() 内存在零点,在区间
内存在零点,在区间![]() 内也存在零点.则
内也存在零点.则![]() 在区间
在区间![]() 内至少有两个零点,由(II)可知,列出不等式组,即可求解.
内至少有两个零点,由(II)可知,列出不等式组,即可求解.
(I)![]() 时,
时,![]() ,
,![]() ,
,![]()
∴切线斜率![]() ,切点坐标
,切点坐标![]() ∴切线方程
∴切线方程![]()
∵切线经过点![]() ,∴
,∴![]() ∴
∴ ![]()
(II)∵![]() ∴
∴![]() .
.
∵![]() 在
在![]() 单调递增,∴
单调递增,∴![]()
![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 单调递增区间为
单调递增区间为![]()
②当![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 单调递减区间为
单调递减区间为![]()
③当![]() 时,令
时,令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
∴函数![]() 单调递减区间为
单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]()
综上①②③可得:
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ;
;
当![]() 时,
时,![]() 单调递减区间为
单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
当![]() 时,
时,![]() 单调递减区间为
单调递减区间为![]() .
.
(Ⅲ)由![]() 得:
得:![]() ,∴
,∴![]()
由已知,设![]() 为
为![]() 在区间
在区间![]() 内的一个零点,
内的一个零点,
则由![]() 可知,
可知,![]() 在区间
在区间![]() 上至少有三个单调区间.
上至少有三个单调区间.
∴![]() 在区间
在区间![]() 内存在零点,在区间
内存在零点,在区间![]() 内也存在零点.
内也存在零点.
∴![]() 在区间
在区间![]() 内至少有两个零点.
内至少有两个零点.
由(II)可知,
当![]() 时,
时,![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 在
在![]() 内至多有一个零点,不合题意.
内至多有一个零点,不合题意.
当![]() 时,
时,![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 在
在![]() 内至多有一个零点,不合题意.
内至多有一个零点,不合题意.
∴![]() ,
,
此时![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增
上单调递增
∴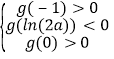
∵![]() ∴
∴![]()
令![]() ,∵
,∵![]() ∴
∴![]() ,
,![]()
令 ![]()
∵![]() ,令
,令![]() 得
得![]() ;令
;令![]() 得
得![]() ;
;
∴![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
∴![]() 在
在![]() 恒成立.
恒成立.
即![]() 在
在![]() 时恒成立.
时恒成立.
∴由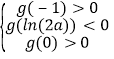 得
得 ,∴
,∴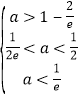 ∴
∴ ![]()
∴![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线交于
,且与抛物线交于![]() 两点.
两点.

(1)求抛物线的焦点![]() 的坐标及准线
的坐标及准线![]() 的方程;
的方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 轴于点
轴于点![]() .证明
.证明![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行六面体ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,点M、F分别是线段AA1、BC的中点.

(1)求证:AF⊥DD1;
(2)求证:AF∥平面MBC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知双曲线
中,已知双曲线![]() .
.
(1)过曲线![]() 的左顶点作
的左顶点作![]() 的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
(2)设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 与圆
与圆![]() 相切,求证:
相切,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的正弦值;
所成二面角的正弦值;
(Ⅲ)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正整数![]() ,设长方形
,设长方形![]() 的边长
的边长![]() ,
,![]() ,边
,边![]() 、
、![]() 、
、![]() 上的点
上的点![]() ,
,![]() …,
…,![]() ,
,![]() ,
,![]() …,
…,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分别满足
分别满足![]() ,
,![]() ,
, ![]() .
.
(1)对于![]() ,2,…,
,2,…,![]() ,求
,求![]() 与
与![]() 、
、![]() 与
与![]() 的交点所在的二次曲线
的交点所在的二次曲线![]() 的方程;
的方程;
(2)若![]() 的延长线上的点
的延长线上的点![]() ,
,![]() ,…,
,…,![]() 满足
满足![]() ,对于
,对于![]() ,2,…,
,2,…,![]() ,求
,求![]() 与
与![]() 的交点所在的二次曲线
的交点所在的二次曲线![]() 的方程;
的方程;
(3)设在二次曲线![]() 上到
上到![]() 的距离最大的点为
的距离最大的点为![]() ,求
,求![]() 与二次曲线
与二次曲线![]() 上的点的距离的最小值.
上的点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年双11当天,某购物平台的销售业绩高达2135亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
(2)若针对服务的好评率,采用分层抽样的方式从这200次交易中取出4次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
附:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com