
【题目】已知某运动员每次投篮命中的概率是40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定l,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下10组随机数:907 966 191 925 271 431 932 458 569 683.
据此估计,该运动员三次投篮恰有两次命中的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】对于![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在首项为-1的等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足
满足
![]() ?若存在,求出
?若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列![]() 是“K数列”,数列
是“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,试判断数列
,试判断数列![]() 是否为“K数列”,并说明理由.
是否为“K数列”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
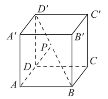
【题目】如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小.
(2)求DP与平面AA′D′D所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()

(Ⅰ)证明:![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(Ⅱ)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为积极响应国家“阳光体育运动”的号召,某学校在了解到学生的实际运动情况后,发起以“走出教室,走到操场,走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况,从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样,收集300位学生每周平均体育运动时间的样本数据(单位:小时),得到如图所示的频率分布直方图。

(1)据图估计该校学生每周平均体育运动时间.并估计高一年级每周平均体育运动时间不足4小时的人数;
(2)规定每周平均体育运动时间不少于6小时记为“优秀”,否则为“非优秀”,在样本数据中,有30位高三学生的每周平均体育运动时间不少于6小时,请完成下列![]() 列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
基础年级 | 高三 | 合计 | |
优秀 | |||
非优秀 | |||
合计 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com