
【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,且
是菱形,且![]() ,其对角线
,其对角线![]() 、
、![]() 交于点
交于点![]() ,
, ![]() 、
、![]() 是棱
是棱![]() 、
、![]() 上的中点.
上的中点.
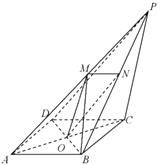
(1)求证:面![]() 面
面![]() ;
;
(2)若面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由![]() 是菱形可得
是菱形可得![]() ,又
,又![]() ,所以
,所以![]() ,于是可得
,于是可得![]() 平面
平面![]() ;又由
;又由![]() 可得
可得![]() 平面
平面![]() ,从而可得平面
,从而可得平面![]() 面
面![]() .(2)在
.(2)在![]() 中由余弦定理可得
中由余弦定理可得![]() ,于是
,于是![]() ,可得
,可得![]() .根据题意可得点
.根据题意可得点![]() 到面
到面![]() 的距离即为点
的距离即为点![]() 到
到![]() 的距离,且为
的距离,且为![]() ,又根据题意得点
,又根据题意得点![]() 到面
到面![]() 的距离为点
的距离为点![]() 到面
到面![]() 的距离的一半,可得
的距离的一半,可得![]() .
.
试题解析:
(1)证明:因为底面![]() 是菱形,
是菱形,
所以![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
又![]() 、
、![]() 是棱
是棱![]() 、
、![]() 上的中点,
上的中点,
所以![]() ,
,
所以![]() ,
,
又![]()
![]()
![]() 面
面![]() ,
, ![]()
![]()
![]() 面
面![]() ,
,
所以![]() 平面
平面![]() .
.
又在![]() 中,
中, ![]() ,且
,且![]()
![]()
![]() 面
面![]() ,
, ![]()
![]()
![]() 面
面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() ,
,
所以平面![]() 面
面![]() .
.
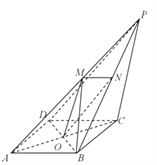
(2)解:在![]() 中,
中, ![]() ,
,
所以![]() ,
,
由(1)知![]() ,
, ![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为平面![]() 底面
底面![]() ,平面
,平面![]()
![]() 底面
底面![]() ,
,
所以点![]() 到面
到面![]() 的距离即为点
的距离即为点![]() 到
到![]() 的距离.
的距离.
又在菱形![]() 中,
中, ![]() ,
, ![]() ,
,
所以点![]() 到
到![]() 的距离为
的距离为![]() ,
,
因为![]() 、
、![]() 、
、![]() 是
是![]() 、
、![]() 、
、![]() 的中点,平面
的中点,平面![]() 面
面![]() ,
,
所以点![]() 到面
到面![]() 的距离为点
的距离为点![]() 到面
到面![]() 的距离的一半,
的距离的一半,
所以![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
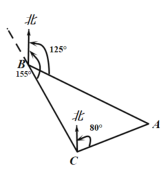
【题目】如图,货轮在海上B处,以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行,为了确定船位,在B点处观测到灯塔A的方位角为125o.半小时后,货轮到达C点处,观测到灯塔A的方位角为80o.求此时货轮与灯塔之间的距离(答案保留最简根号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( )
A.已知直线![]() 和平面
和平面![]() ,若点
,若点![]() ,点
,点![]() 且
且![]() ,
,![]() ,则
,则![]()
B.若三条直线两两相交,则三条直线确定一个平面
C.若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,则
,则![]() 内的所有直线与
内的所有直线与![]() 都不相交
都不相交
D.若直线![]() 和
和![]() 不平行,且
不平行,且![]() ,
,![]() ,
,![]() ,则l至少与
,则l至少与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率是40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定l,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下10组随机数:907 966 191 925 271 431 932 458 569 683.
据此估计,该运动员三次投篮恰有两次命中的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88,若样本B数据恰好是样本A数据都加上2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 的右顶点,过点
的右顶点,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
, ![]() 两点.求证:点
两点.求证:点![]() 在以
在以![]() 为直径的圆上.
为直径的圆上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com