
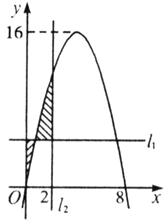
(1)求a、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若g(x)=6lnx+m,问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
解:(1)由图形知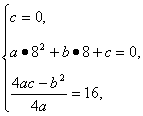 解之得
解之得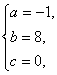
∴函数f(x)的解析式为f(x)=-x2+8x.
(2)由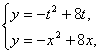 得x2-8x-t(t-8)=0,∴x1=t,x2=8-t.
得x2-8x-t(t-8)=0,∴x1=t,x2=8-t.
∵0≤t≤2,
∴直线l1与f(x)的图象的交点坐标为(t,-t2+8t).
由定积分的几何意义知:
S(t)=![]() dx+
dx+![]() dx
dx
=[(-t2+8t)x-(![]() +
+![]() )]
)]![]() +[(
+[(![]() +
+![]() )-(-t2+8t)·x
)-(-t2+8t)·x![]() =
=![]() t3+10t2-16t+
t3+10t2-16t+![]() .
.
(3)令φ(x)=g(x)-f(x)=x2-8x+6lnx+m.
∵x>0,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数φ(x)=x2-8x+6lnx+m的图象与x轴的正半轴有且只有两个不同的交点,
∴φ′(x)=2x-8+![]() =
=![]() =
=![]() (x>0).
(x>0).
当x∈(0,1)时,φ′(x)>0,φ(x)是增函数;
当x∈(1,3)时,φ′(x)<0,φ(x)是减函数;
当x∈(3,+∞)时,φ′(x)>0,φ(x)是增函数;
当x=1或x=3时,φ′(x)=0,
∴φ(x)的极大值为φ(1)=m-7;
φ(x)的极小值为φ(3)=m+6ln3-15.
又∵当x→0时,φ(x)→-∞,
当x→+∞时,φ(x)→+∞,
∴要使φ(x)=0有且仅有两个不同的正根,必须且只需
![]() 或
或![]()
即![]() 或
或![]()
∴m=7或m=15-6ln3.
∴当m=7或m=15-6ln3时,函数f(x)与g(x)的图象有且只有两个不同交点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| x |
| 1 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bx-1 | a2x+2b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bx-1 | a2x+2b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com