
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,
,![]() 面
面![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
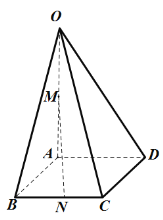
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1) 取![]() 的中点
的中点![]() ,构造平行四边形
,构造平行四边形![]() ,再根据线面平行的判定定理完成证明;
,再根据线面平行的判定定理完成证明;
(2)根据平行可知异面直线![]() 与
与![]() 所成的角即为
所成的角即为![]() 或其补角,然后根据长度进行求解;
或其补角,然后根据长度进行求解;
(3)根据线面平行将问题转化为![]() 到平面
到平面![]() 的距离,然后作出
的距离,然后作出![]() 在平面内的射影,根据长度即可计算出
在平面内的射影,根据长度即可计算出![]() 到平面
到平面![]() 的距离,即可求解出点
的距离,即可求解出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .则四边形
.则四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,又∵
,又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
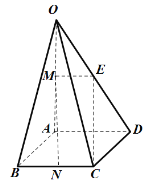
(2)∵![]() ,
,
∴![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角(或其补角)
所成的角(或其补角)
作![]() 于点
于点![]() ,连接
,连接![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
所以异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.

(3)∵![]() 平面
平面![]() ,∴点
,∴点![]() 和点
和点![]() 到平面
到平面![]() 的距离相等.
的距离相等.
连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
线段![]() 的长就是点
的长就是点![]() 到平面
到平面![]() 的距离,与点
的距离,与点![]() 到平面
到平面![]() 的距离相等
的距离相等
![]() ,
,![]() ,
,
 .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.



 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() 分别为
分别为![]() 的中点
的中点![]()
![]() 为
为![]() 中点,现将四边形
中点,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体,在图②中.
,得到如图②所示的多面体,在图②中. 
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A.一条直线和直线外一点确定一个平面
B.平行于同一平面的两个不同平面平行
C.若直线![]() 不平行平面
不平行平面![]() ,则在平面
,则在平面![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D.如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.

(1)求证:图2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)将红色卡片和蓝色卡片分别放在两个袋中,然后从两个袋中各取一张卡片,求两张卡片数字之积为偶数的概率
(2)将五张卡片放在一个袋子中,从中任取两张,求两张卡片颜色不同的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com