【题目】“沉鱼、落雁、闭月、羞花”是由精彩故事组成的历史典故．“沉鱼”，讲的是西施浣纱的故事；“落雁”，指的就是昭君出塞的故事；“闭月”，是述说貂蝉拜月的故事；“羞花”，谈的是杨贵妃醉酒观花时的故事．她们分别是中国古代的四大美女．某艺术团要以四大美女为主题排演一部舞蹈剧，已知乙扮演杨贵妃，甲、丙、丁三人抽签决定扮演的对象，则甲不扮演貂蝉且丙扮演昭君的概率为______．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】边长为
的等边三角形内任一点到三边距离之和为定值，这个定值等于
；将这个结论推广到空间是：棱长为的正四面体内任一点到各面距离之和等于________________.（具体数值）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】改革开放以来，我国经济持续高速增长
如图给出了我国2003年至2012年第二产业增加值与第一产业增加值的差值
以下简称为：产业差值
的折线图，记产业差值为
单位：万亿元．
求出y关于年份代码t的线性回归方程；
利用中的回归方程，分析2003年至2012年我国产业差值的变化情况，并预测我国产业差值在哪一年约为34万亿元；
结合折线图，试求出除去2007年产业差值后剩余的9年产业差值的平均值及方差结果精确到
．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：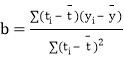
，
．
样本方差公式：
．
参考数据：
，
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为
，
为抛物线
上异于原点的任意一点，过点的直线
交抛物线于另一点
，交
轴的正半轴于点
，且有
.当点的横坐标为3时，
为正三角形.
（1）求抛物线的方程；
（2）若直线
，且
和抛物线有且只有一个公共点
，试问直线
是否过定点，若过定点，求出定点坐标；若不过定点，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在由数字1，2，3，4，5组成的所有没有重复数字的四位数中，大于3145且小于4231的数共有（ ）
A.27个B.28个C.29个D.30个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4-4：坐标系与参数方程]
在平面直角坐标系
中，直线
的参数方程为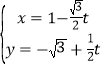
（
为参数），以坐标原点为极点，
轴的非负半轴为极轴，建立极坐标系，曲线
的极坐标方程为
．
（1）求直线的普通方程及曲线的直角坐标方程；
（2）设点
，直线与曲线相交于两点
，
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】研究机构对某校学生往返校时间的统计资料表明：该校学生居住地到学校的距离
（单位：千米）和学生花费在上学路上的时间
（单位：分钟）有如下的统计资料：
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明与有线性相关关系，试求：
（1）判断与是否有很强的线性相关性？
（相关系数
的绝对值大于0.75时，认为两个变量有很强的线性相关性，精确到0.01）
（2）求线性回归方程
（精确到0.01）；
（3）将
分钟的时间数据
称为美丽数据，现从这6个时间数据中任取2个，求抽取的2个数据全部为美丽数据的概率.
参考数据：
，
，
，
，
，
参考公式：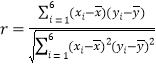
，
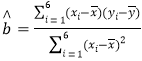
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
