
【题目】已知![]() ,函数
,函数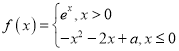 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.若![]() ,则
,则![]() 的图象上存在唯一一对关于原点
的图象上存在唯一一对关于原点![]() 对称的点
对称的点
B.存在实数![]() 使得
使得![]() 的图象上存在两对关于原点
的图象上存在两对关于原点![]() 对称的点
对称的点
C.不存在实数![]() 使得
使得![]() 的图象上存在两对关于
的图象上存在两对关于![]() 轴对称的点
轴对称的点
D.若![]() 的图象上存在关于
的图象上存在关于![]() 轴对称的点,则
轴对称的点,则![]()
科目:高中数学 来源: 题型:
【题目】某学校课外兴趣小组利用假期到植物园开展社会实践活动,研究某种植物生长情况与温度的关系.现收集了该种植物月生长量y(cm)与月平均气温x(℃)的8组数据,并制成如图所示的散点图.
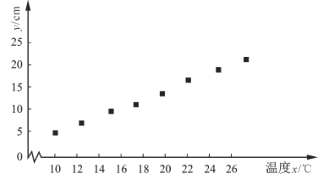
根据收集到的数据,计算得到如下值:
|
|
|
|
18 | 12.325 | 224.04 | 235.96 |
(1)求出y关于x的线性回归方程(最终结果的系数精确到0.01),并求温度为28℃时月生长量y的预报值;
(2)根据y关于x的回归方程,得到残差图如图所示,分析该回归方程的拟合效果.

附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右两个焦点为
的左,右两个焦点为![]() 、
、![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 有公共焦点
有公共焦点![]() .且两曲线
.且两曲线![]() 、
、![]() 在第一象限的交点
在第一象限的交点![]() 的横坐标为
的横坐标为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 为坐标原点),与椭圆
为坐标原点),与椭圆![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 在线段
在线段![]() 上),且
上),且![]() .问满足条件的直线
.问满足条件的直线![]() 有几条,说明理由.
有几条,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最大值为
的最大值为![]() ;
;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 在区间
在区间![]() 单调递增.
单调递增.
其中所有正确结论的编号是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线的准线与
是抛物线的准线与![]() 轴的交点,直线
轴的交点,直线![]() 经过焦点
经过焦点![]() 且与抛物线相交于
且与抛物线相交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,记
两点,记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() .
.
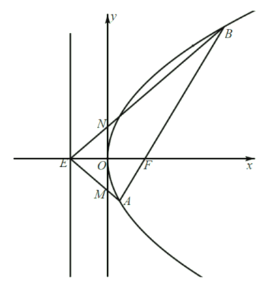
(1)求证: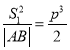 ;
;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,以线段
两点,以线段![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 、
、![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,则( )
,则( )
A.![]()
B.若![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]()
C.若抛物线上存在一点![]() 到焦点
到焦点![]() 的距离等于
的距离等于![]() ,则抛物线的方程为
,则抛物线的方程为![]()
D.若点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() ,则
,则![]() 的最小值为
的最小值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com