Question

【题目】已知函数f（x）=alnx+ x2﹣ax（a为常数）有两个极值点．
（1）求实数a的取值范围；
（2）设f（x）的两个极值点分别为x1 ， x2 ， 若不等式f（x1）+f（x2）＜λ（x1+x2）恒成立，求λ的最小值．

Answer 1

【答案】
（1）解：由题设知，函数f（x）的定义域为（0，+∞），

f′（x）= 且f′（x）=0有两个不同的正根，即x2﹣ax+a=0两个不同的正根x1，x2，（x1＜x2）

则 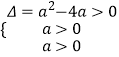，∴a＞4，

（0，x1），f′（x）＞0，（x1，x2），f′（x）＜0，（x2，+∞），f′（x）＞0，

∴x1，x2是f（x）的两个极值点，符合题意，

∴a＞4；

（2）解：f（x1）+f（x2）=alnx1+ x12﹣ax1+alnx2+ x22﹣ax2=a（lna﹣ a﹣1），

∴ =lna﹣ a﹣1，

令y=lna﹣ a﹣1，则y′= ﹣ ，

∵a＞4，

∴y′＜0，

∴y=lna﹣ a﹣1在（4，+∞）上单调递减，

∴y＜ln4﹣3，

∵不等式f（x1）+f（x2）＜λ（x1+x2）恒成立，x1+x2＞0，

∴是λ的最小值ln4﹣3

【解析】（1）f′（x）= 且f′（x）=0有两个不同的正根，即x2﹣ax+a=0两个不同的正根，即可求实数a的取值范围；（2）利用韦达定理，可得 =lna﹣ a﹣1，构造函数，确定函数的单调性，求出其范围，即可求λ的最小值．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能正确解答此题．