
【题目】已知锐角△ABC中内角A、B、C所对边的边长分别为a、b、c,满足a2+b2=6abcosC,且 ![]() .
.
(1)求角C的值;
(2)设函数 ![]() ,图象上相邻两最高点间的距离为π,求f(A)的取值范围.
,图象上相邻两最高点间的距离为π,求f(A)的取值范围.
【答案】
(1)解:因为a2+b2=6abcosC,由余弦定理知a2+b2=c2+2abcosC,
所以 ![]()
又因为sin2C=2 ![]() sinAsinB,则由正弦定理得:c2=2
sinAsinB,则由正弦定理得:c2=2 ![]() ab,
ab,
所以cosC= ![]() =
= ![]() =
= ![]() ,
,
所以C= ![]() .
.
(2)解:因为 ![]() ,
,
由已知 ![]() =π,ω=2,
=π,ω=2,
则 ![]() ,
,
因为 ![]() ,
, ![]() ,
,
由于0 ![]() ,0
,0 ![]() ,
,
所以 ![]() .
.
所以 ![]() ,
,
所以 ![]() .
.
【解析】(1)由a2+b2=6abcosC,结合余弦定理可求 ![]() ,又sin2C=2
,又sin2C=2 ![]() sinAsinB,根据由正弦定理得:c2=2
sinAsinB,根据由正弦定理得:c2=2 ![]() ab,从而可求cosC,即可解得C的值.(2)由三角函数恒等变换的应用化简函数解析式可得
ab,从而可求cosC,即可解得C的值.(2)由三角函数恒等变换的应用化简函数解析式可得 ![]() ,由题意,利用周期公式即可求ω,可得
,由题意,利用周期公式即可求ω,可得 ![]() ,由
,由 ![]() ,
, ![]() ,A,B为锐角,可得范围
,A,B为锐角,可得范围 ![]() ,求得范围
,求得范围 ![]() ,利用正弦函数的图象和性质即可得解.
,利用正弦函数的图象和性质即可得解.
【考点精析】利用正弦定理的定义和余弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】经过市场调查,超市中的某种小商品在过去的近40天的日销售量(单位:件)与价格(单位:元)为时间![]() (单位:天)的函数,且日销售量近似满足
(单位:天)的函数,且日销售量近似满足![]() ,价格近似满足
,价格近似满足![]() 。
。
(1)写出该商品的日销售额![]() (单位:元)与时间
(单位:元)与时间![]() (
(![]() )的函数解析式并用分段函数形式表示该解析式(日销售额=销售量
)的函数解析式并用分段函数形式表示该解析式(日销售额=销售量![]() 商品价格);
商品价格);
(2)求该种商品的日销售额![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定长为2的线段AB的两个端点在以点(0, ![]() )为焦点的抛物线x2=2py上移动,记线段AB的中点为M,求点M到x轴的最短距离,并求此时点M的坐标。
)为焦点的抛物线x2=2py上移动,记线段AB的中点为M,求点M到x轴的最短距离,并求此时点M的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河北保定市上学期期末调研】已知点![]() 到点
到点![]() 的距离比到
的距离比到![]() 轴的距离大1.
轴的距离大1.
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)设直线![]() :
: ![]() ,交轨迹
,交轨迹![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 为坐标原点,试在轨迹
为坐标原点,试在轨迹![]() 的
的![]() 部分上求一点
部分上求一点![]() ,使得
,使得![]() 的面积最大,并求其最大值.
的面积最大,并求其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发一种新药, 成年人按规定的剂量服用后, 每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间关系满足如图所示的曲线.
(小时)之间关系满足如图所示的曲线.
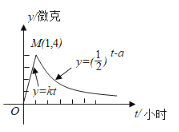
(1)写出![]() 关于
关于![]() 的函数关系式:
的函数关系式:![]() ;
;
(2)据进一步测定: 每毫升血液中的含药量不少于![]() 微克时, 治疗疾病有效. 求服药一次后治疗疾病有效的时间.
微克时, 治疗疾病有效. 求服药一次后治疗疾病有效的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com