
(14分)已知定义在R上的函数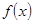 对任意
对任意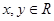 都有
都有
 ,且当
,且当 时,
时,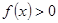
(1)求证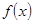 为奇函数;
为奇函数;
(2)判断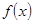 在R上的单调性,并用定义证明;
在R上的单调性,并用定义证明;
(3)若 ,对任意
,对任意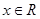 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
20.(1)证明: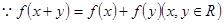 ①
①
令x=y=0,代人①式,得 ,即
,即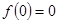 ;-----------(1分)
;-----------(1分)
令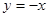 ,代人①式,得
,代人①式,得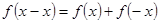 ,又
,又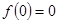 ,则有
,则有
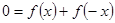 ,即
,即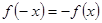 对任意
对任意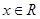 成立,---------------(3分)
成立,---------------(3分)
所以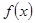 为奇函数;---------------------------------------------(4分)
为奇函数;---------------------------------------------(4分)
(2)解: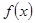 在R上的单调递增,以下用定义证明:
在R上的单调递增,以下用定义证明:
设任意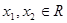 ,且
,且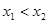 ,则
,则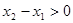 ,所以
,所以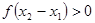 --------(5分)
--------(5分)
即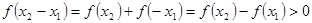 ----------------------(7分)
----------------------(7分)
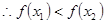 ,
,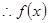 在R上的单调递增;------------------------(8分)
在R上的单调递增;------------------------(8分)
(3)由(1)(2)可知,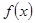 是在R上的单调递增的奇函数,
是在R上的单调递增的奇函数,
故由 可得
可得
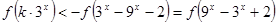 --------------------------(9分)
--------------------------(9分)
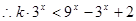 即
即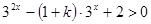 对任意
对任意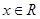 恒成立。-------(10分)
恒成立。-------(10分)
令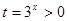 ,问题等价于
,问题等价于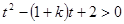 对任意
对任意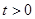 恒成立。
恒成立。
令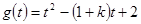 ,其对称轴为
,其对称轴为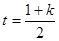 ,-----------------------(11分)
,-----------------------(11分)
当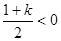 即
即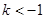 时,
时,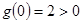 ,符合题意;-------------------(12分)
,符合题意;-------------------(12分)
当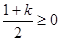 时,对任意
时,对任意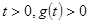 恒成立
恒成立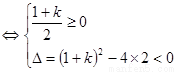
解得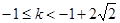 -------------------------------------------(13分)
-------------------------------------------(13分)
综上所述,
当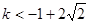 时,
时, ,对任意
,对任意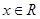 恒成立。--(14分)
恒成立。--(14分)
(3)解法二:由(1)(2)可知,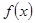 是在R上的单调递增的奇函数,
是在R上的单调递增的奇函数,
故由 可得
可得
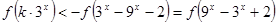 -----------------------------(9分)
-----------------------------(9分)
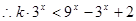 ---------------------------------------------
(10分)
---------------------------------------------
(10分)
即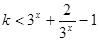 ------------------------------------------------ (11分)
------------------------------------------------ (11分)
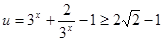 ,当且仅当
,当且仅当 时,等号成立
时,等号成立
即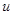 的最小值为
的最小值为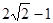 ;------------------ (12分)
;------------------ (12分)
要使对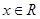 不等式
不等式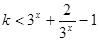 恒成立,只要使
恒成立,只要使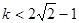 ;------ (13分)
;------ (13分)
即当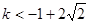 时,
时, ,对任意
,对任意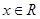 恒成立。(14分)
恒成立。(14分)
【解析】略


科目:高中数学 来源: 题型:
(本小题满分14分)已知定义在![]() 上的函数
上的函数![]() 同时满足:①对任意
同时满足:①对任意![]() ,都有
,都有![]() ②当
②当![]() 时,
时,![]() ,试解决下列问题: (Ⅰ)求在
,试解决下列问题: (Ⅰ)求在![]() 时,
时,![]() 的表达式;(Ⅱ)若关于
的表达式;(Ⅱ)若关于![]() 的方程
的方程![]() 在
在![]() 上有实数解,求实数
上有实数解,求实数![]() 的取值范围;(Ⅲ)若对任意
的取值范围;(Ⅲ)若对任意![]() ,关于
,关于![]() 的不等式
的不等式![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012届广东省珠海市高三第一次月考理科数学 题型:解答题
.(本小题满分14分)已知定义在 上的奇函数
上的奇函数 满足
满足 ,且对任意
,且对任意 有
有 .
.
(Ⅰ)判断 在
在 上的奇偶性,并加以证明.
上的奇偶性,并加以证明.
(Ⅱ)令 ,
, ,求数列
,求数列 的通项公式.
的通项公式.
(Ⅲ)设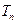 为
为 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三上学期第三次月考文科数学 题型:解答题
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三上学期期中考试文科数学 题型:解答题
(本题满分14分)已知定义在R上的函数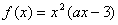 ,其中a为常数.
,其中a为常数.
(1)若x=1是函数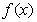 的一个极值点,求a的值;
的一个极值点,求a的值;
(2)若函数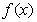 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(3)若函数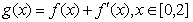 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012届安徽省蚌埠铁中高三上学期期中考试文科数学 题型:解答题
(本题满分14分)已知定义在R上的函数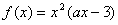 ,其中a为常数.
,其中a为常数.
(1)若x=1是函数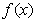 的一个极值点,求a的值;
的一个极值点,求a的值;
(2)若函数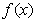 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(3)若函数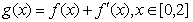 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com