
【题目】解答
(1)用反证法证明:已知实数a,b,c满足a+b+c=1,求证:a、b、c中至少有一个数不大于 ![]()
(2)用分析法证明: ![]() +
+ ![]() >2
>2 ![]() +
+ ![]() .
.
【答案】
(1)证明:假设a、b、c都大于 ![]() ,则a+b+c>1,这与已知a+b+c=1矛盾.
,则a+b+c>1,这与已知a+b+c=1矛盾.
故a、b、c中至少有一个不大于 ![]()
(2)证明:要证 ![]() +
+ ![]() >2
>2 ![]() +
+ ![]() ,
,
只要证 6+7+2 ![]() >8+5+4
>8+5+4 ![]() ,
,
只要证 ![]() >2
>2 ![]() ,
,
即证42>40.
而42>40 显然成立,
故原不等式成立
【解析】(1)根据题意,通过反证法假设结论不成立,通过得出与已知a+b+c=1矛盾,可得结论;(2)寻找使不等式成立的充分条件,要是不等式成立,只要证 6+7+2 ![]() >8+5+4
>8+5+4 ![]() ,即证
,即证 ![]() >2
>2 ![]() ,
,
即证 42>40.
【考点精析】通过灵活运用反证法与放缩法,掌握常见不等式的放缩方法:①舍去或加上一些项②将分子或分母放大(缩小)即可以解答此题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x)其中(a>0且a≠1),设h(x)=f(x)﹣g(x).
(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,
, ![]() :
: ![]() ,
, ![]() :
: ![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() .
.
(1)求点![]() 的极坐标;
的极坐标;
(2)若直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于两不同的点
交于两不同的点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)过点(1,
(a>b>0)过点(1, ![]() ),离心率为
),离心率为 ![]() ,过椭圆右顶点A的两条斜率乘积为﹣
,过椭圆右顶点A的两条斜率乘积为﹣ ![]() 的直线分别交椭圆C于M,N两点.
的直线分别交椭圆C于M,N两点.
(1)求椭圆C的标准方程;
(2)直线MN是否过定点D?若过定点D,求出点D的坐标;若不过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设有正整数![]() ,使得
,使得![]() 成等差数列,求
成等差数列,求![]() 的值;
的值;
(3)设![]() ,对于给定的
,对于给定的![]() ,求三个数
,求三个数![]() 经适当排序后能构成等差数列的充要条件.
经适当排序后能构成等差数列的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() .
.
(1)求函数f(x)的定义域和值域;
(2)设F(x)= ![]() [f2(x)﹣2]+f(x)(a为实数),求F(x)在a<0时的最大值g(a);
[f2(x)﹣2]+f(x)(a为实数),求F(x)在a<0时的最大值g(a);
(3)对(2)中g(a),若﹣m2+2tm+ ![]() ≤g(a)对a<0所有的实数a及t∈[﹣1,1]恒成立,求实数m的取值范围.
≤g(a)对a<0所有的实数a及t∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆的离心率为![]() ,且点
,且点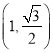 在椭圆上,①求椭圆的方程;
在椭圆上,①求椭圆的方程;
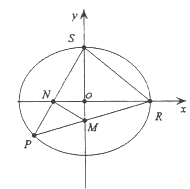
②设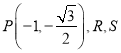 分别为椭圆
分别为椭圆![]() 的右顶点和上顶点,直线
的右顶点和上顶点,直线![]() 和
和![]() 与
与![]() 轴和
轴和![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程;
的方程;
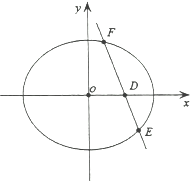
(2)设 ![]() 过
过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 均在
均在![]() 的右侧,
的右侧, ![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①用反证法证明命题“a,b∈R,方程x3+ax+b=0至少有一个实根”时,要作的假设是“方程至多有两个实根”;
②用数学归纳法证明“1+2+22+…+2n+2=2n+3﹣1,在验证n=1时,左边的式子是1+2+22;
③用数学归纳法证明 ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() (n∈N*)的过程中,由n=k推导到n=k+1时,左边增加的项为
(n∈N*)的过程中,由n=k推导到n=k+1时,左边增加的项为 ![]() +
+ ![]() ,没有减少的项;
,没有减少的项;
④演绎推理的结论一定正确;
⑤要证明“ ![]() ﹣
﹣ ![]() >
> ![]() ﹣
﹣ ![]() ”的最合理的方法是分析法.
”的最合理的方法是分析法.
A.①④
B.④
C.②③⑤
D.⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各小题中,P是q的充要条件的是(08年山东理改编)
1)p:m<﹣2或m>6;q:y=x2+mx+m+3有两个不同的零点.
2)p: ![]() =1,q:y=f(x)是偶函数.
=1,q:y=f(x)是偶函数.
3)p:cosα=cosβ,q:tanα=tanβ.
4)p:A∩B=A,q:CUBCUA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com