练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知中心在原点，焦点在x轴上的椭圆的一个顶点坐标为（0，1），其离心率为
    （1）求椭圆的标准方程；
    （2）椭圆上一点P满足∠F1PF2=60°，其中F1 ， F2为椭圆的左右焦点，求△F1PF2的面积．

    【答案】
    （1）

    解：设椭圆的标准方程为 （a＞b＞0），

    椭圆的一个顶点为（0，1）则b=1，

    由椭圆的离心率e= = = ，解得：a2=3，

    椭圆的标准方程为


    （2）

    解：设丨PF1丨=n，丨PF2丨=m，∠F1PF2=60°，

    由余弦定理可知：丨F1F2丨2=丨PF1丨2+丨PF2丨2﹣2丨PF1丨丨PF1丨cos60°，

    4c2=m2+n2﹣2mncos60°=（m+n）2﹣3mn=4a2﹣3mn，

    则4×（ ）2=4a2﹣3mn，解得：mn= ，

    即丨PF1丨丨PF1丨= ，

    △F1PF2的面积S= ×丨PF1丨丨PF1丨×sin∠F1PF2，

    ∴ ，

    △F1PF2的面积


    【解析】（1）设椭圆的方程，则b=1，根据椭圆的离心率即可求得a的值，即可求得椭圆方程；（2）根据余弦定理，即可求得丨PF1丨丨PF1丨，利用三角形的面积公式即可求得△F1PF2的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】解答题
    （1）已知x+x﹣1=3，求下列各式 ，x2+x﹣2的值；
    （2）求值：（lg2）2+lg2lg50+lg25．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（文科做）已知函数f（x）=x﹣ ﹣（a+2）lnx，其中实数a≥0．
    （1）若a=0，求函数f（x）在x∈[1，3]上的最值；
    （2）若a＞0，讨论函数f（x）的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （Ⅰ）当时，求函数的单调区间；

    （Ⅱ）当，时，证明：（其中为自然对数的底数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费（单位:千元)对年销售量（单位: )和年利润（单位:千元)的影响.对近8年的年宣传费和年销售量数据作了初步处理，得到下面的散点图及一些统计量的值.

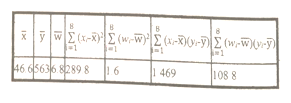
    表中.

    （1）根据散点图判断与哪一个适宜作为年销售量关于年宣传费的回归类型？（给出判断即可，不必说明理由）

    （2）根据（1）的判断结果及表中数据，建立关于的回归方程；

    （3）已知这种产品的利润与的的关系为.根据（2）的结果回答下列问题：

    （ⅰ）年宣传费时，年销售量及年利润的预报值是多少？

    （ⅱ）年宣传费为何值时，年利润的预报值最大？

    附:对于一组数据，其回归直线的的斜率和截距的最小二乘估计为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    (1)求函数的单调区间；

    (2)若函数有两个零点，()，求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，有一块半径长为1米的半圆形钢板，现要从中截取一个内接等腰 梯形部件ABCD，设梯形部件ABCD的面积为平方米．

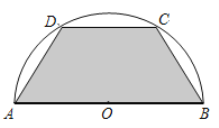
    （1）按下列要求写出函数关系式：

    ①设（米），将表示成的函数关系式；

    ②设，将表示成的函数关系式．

    （2）求梯形部件ABCD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A,B,C所对的边分别是a,b,c,且.

    （Ⅰ）证明：；

    （Ⅱ）若，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是首项为正数的等差数列，a1a2=3，a2a3=15．
    （1）求数列{an}的通项公式；
    （2）设bn=（an+1）2 ，求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    同步练习册答案