
【题目】已知圆C经过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上,又直线
上,又直线![]() 与圆C交于P,Q两点.
与圆C交于P,Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数
,求实数![]() 的值;
的值;
(3)过点![]() 作直线
作直线![]() ,且
,且![]() 交圆C于M,N两点,求四边形
交圆C于M,N两点,求四边形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)x 2 +y 2 =4(2)k=0(3)7
【解析】试题分析:(1)设圆心为![]() ,半径为
,半径为![]() .故
.故![]() ,建立方程,从而可求圆
,建立方程,从而可求圆![]() 的方程;(2)利用向量的数量积公式,求得
的方程;(2)利用向量的数量积公式,求得![]() ,计算圆心到直线
,计算圆心到直线![]() 的距离
的距离![]() ,即可求解实数
,即可求解实数![]() 的值;(3)方法1、设圆
的值;(3)方法1、设圆![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,求得
,求得![]() ,根据垂径定理和勾股定理,可得
,根据垂径定理和勾股定理,可得![]() ,在利用基本不等式,可求四边形
,在利用基本不等式,可求四边形![]() 面积的最大值;方法2、利用弦长公式
面积的最大值;方法2、利用弦长公式![]() ,
, 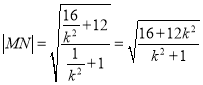 ,表示三角形的面积,在利用基本不等式,可求四边形
,表示三角形的面积,在利用基本不等式,可求四边形![]() 面积的最大值.
面积的最大值.
试题解析:(1)设圆心为![]() ,半径为
,半径为![]() .故
.故![]() ,易得
,易得![]() ,
,
因此圆的方程为![]() .
.
(2)因为![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
故![]() ,
, ![]() ,所以
,所以![]() 到直线
到直线![]() 的距离
的距离![]() ,又
,又![]() ,所以
,所以![]() .
.
又解:设P![]() ,
, ![]() ,则
,则![]() ,即
,即![]() ,
,
由![]() 得
得![]() ,∴
,∴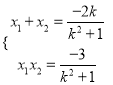 ,
,
代入![]() 得
得![]() ,∴
,∴![]() ;
;
(3)设圆心![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.
因为直线![]() 都经过点
都经过点![]() ,且
,且![]() ,根据勾股定理,有
,根据勾股定理,有![]() ,
,
又![]() ,
,
故![]()
 当且仅当
当且仅当![]() 时,等号成立,所以
时,等号成立,所以![]() .
.
(3)又解:由已知![]() ,由(2)的又解可得
,由(2)的又解可得![]() ,
,
同理可得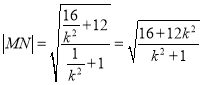 ,
,
∴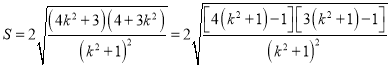
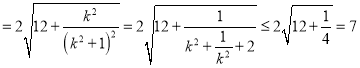 ,
,
当且仅当![]() 时等号成立,所以
时等号成立,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题,某单位在国家科研部门的支持下,进行技术攻关,采用了新式艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() +b,其中a,b是常数且a>0.
+b,其中a,b是常数且a>0.
(1)用函数单调性的定义证明f(x)在区间(0, ![]() ]上是单调递减函数;
]上是单调递减函数;
(2)已知函数f(x)在区间[ ![]() ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
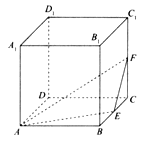
【题目】(文科选做)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E、F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是_____。
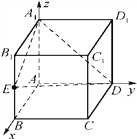
(理科选做)在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x﹣sin4x.下列结论正确的是( )
A.函数f(x)在区间[0, ![]() ]上是减函数
]上是减函数
B.函数f(x)的图象关于原点对称
C.f(x)的最小正周期为 ![]()
D.f(x)的值域为[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且当x=
)的最小正周期是π,且当x= ![]() 时,f(x)取得最大值2.
时,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93,下列说法正确的是( )
A.这种抽样方法是一种分层抽样
B.这种抽样方法是一种系统抽样
C.这五名男生成绩的方差大于这五名女生成绩的方差
D.该班男生成绩的平均数大于该班女生成绩的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() =80,
=80, ![]() =20,
=20, ![]() iyi=184,
iyi=184, ![]()
![]() =720.(b=
=720.(b= 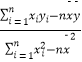 )
)
(1)求家庭的月储蓄y对月收入x的线性回归方程;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com