
【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且当x=
)的最小正周期是π,且当x= ![]() 时,f(x)取得最大值2.
时,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
【答案】
(1)解:因为函数f(x)的最小正周期是π,所以ω=2.
又因为 ![]() 时,f(x)取得最大值2.所以A=2,
时,f(x)取得最大值2.所以A=2,
同时 ![]() ,
, ![]() ,∵
,∵ ![]() ∴
∴ ![]() ,
,
∴函数y=f(x)的解析式 ![]() .
.
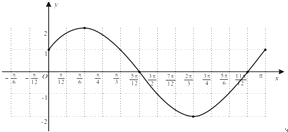
∵x∈[0,π],∴ ![]() ,列表如下:
,列表如下:
|
|
| π |
| 2π |
|
x | 0 |
|
|
|
| x |
f(x) | 1 | 2 | 0 | ﹣2 | 0 | 1 |
描点、连线得下图
(2)解:由已知得y=g(x)=f(x﹣m)= ![]() 是偶函数,
是偶函数,
所以 ![]() ,
, ![]() ,
,
又因为m>0,所以m的最小值为 ![]()
【解析】(1)由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,用五点法作函数y=Asin(ωx+φ)在一个周期上的图象.(2)利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的奇偶性,求得m的最小值.
【考点精析】本题主要考查了五点法作函数y=Asin(ωx+φ)的图象和函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线);图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
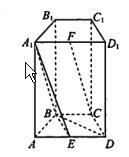
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左焦点为
的左焦点为![]() ,
, ![]() 为坐标原点,点
为坐标原点,点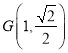 在椭圆上,过点
在椭圆上,过点![]() 的直线
的直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)设过点![]() 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于![]() 两点,
两点, ![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 是菱形的两条邻边,求点
是菱形的两条邻边,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出如图所示的频率分布直方图,已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[100,120]之间的学生人数是( ) 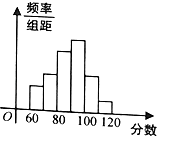
A.32
B.24
C.18
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上,又直线
上,又直线![]() 与圆C交于P,Q两点.
与圆C交于P,Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数
,求实数![]() 的值;
的值;
(3)过点![]() 作直线
作直线![]() ,且
,且![]() 交圆C于M,N两点,求四边形
交圆C于M,N两点,求四边形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(α)= ![]() .
.
(1)若α为第二象限角且f(α)=﹣ ![]() ,求
,求 ![]() 的值;
的值;
(2)若5f(α)=4f(3α+2β).试问tan(2α+β)tan(α+β)是否为定值(其中α≠kπ+ ![]() ,α+β≠kπ+
,α+β≠kπ+ ![]() ,2α+β≠kπ+
,2α+β≠kπ+ ![]() ,3α+2β≠kπ+
,3α+2β≠kπ+ ![]() ,k∈Z)?若是,请求出定值;否则,说明理由.
,k∈Z)?若是,请求出定值;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).

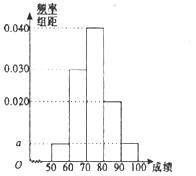
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式: 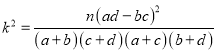 ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且不与
且不与![]() 轴、
轴、![]() 轴垂直,且与圆
轴垂直,且与圆![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 作
作![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线与圆
垂直的直线与圆![]() 交于
交于![]() 两点,求
两点,求![]() 与
与![]() 的面积之和的取值范围.
的面积之和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,an+1﹣an﹣2n﹣2=0(n∈N*).
(1)求数列{an}的通项公式;
(2)设 ![]() ,若对任意的正整数n,当m∈[﹣1,1]时,不等式
,若对任意的正整数n,当m∈[﹣1,1]时,不等式 ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com