
 ,
, ,
, ,
, ,
,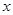 的极差是7,那么
的极差是7,那么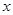 的值是 .
的值是 .科目:高中数学 来源:不详 题型:单选题
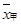 ,
,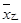 ,中位数分别为m甲,m乙,则
,中位数分别为m甲,m乙,则
A.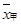 < <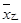 ,m甲> m乙 ,m甲> m乙 | B.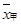 < <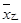 ,m甲< m乙 ,m甲< m乙 |
C.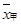 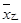 ,m甲> m乙 ,m甲> m乙 | D.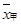 > >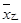 ,m甲< m乙 ,m甲< m乙 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| PM2.5日均值 (微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据:
)如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据: ,
, ;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为
;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为 ,则估计案发嫌疑人的身高为
,则估计案发嫌疑人的身高为 .
.| 脚长 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 身高 | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在 内)
内)
 内的频率;
内的频率; 内的居民中抽取多少人?
内的居民中抽取多少人?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,求
,求 的数学期望.
的数学期望. .则
.则 =0.6826,
=0.6826, ="0.9544,"
="0.9544,"  =0.9974.
=0.9974.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com