
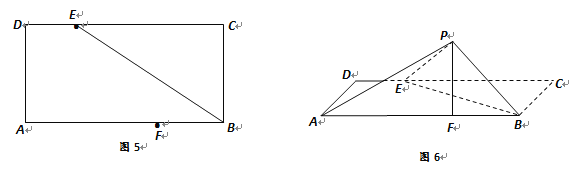
【题目】如图![]() ,矩形
,矩形![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() 边上的点,且
边上的点,且![]() ,将
,将![]() 沿
沿![]() 折起至
折起至![]() 位置(如图
位置(如图![]() 所示),连结
所示),连结![]() ,其中
,其中![]() .
.
(Ⅰ) 求证: ![]() ;
;
(Ⅱ) 在线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(Ⅲ) 求点![]() 到
到![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(Ⅰ)连结EF,由翻折不变性可知,PB=BC=6,PE=CE=9,由已知条件,利用勾股定理推导出PF⊥BF,PF⊥EF,由此能够证明PF⊥平面ABED.
(Ⅱ)当Q为PA的三等分点(靠近P)时,FQ∥平面PBE.由已知条件推导出FQ∥BP,即可证明FQ∥平面PBE.
(Ⅲ)由PF⊥平面ABED,知PF为三棱锥P-ABE的高,利用等积法能求出点A到平面PBE的距离.
试题解析:
(Ⅰ)连结![]() ,由翻折不变性可知,
,由翻折不变性可知, ![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
所以![]()
在图![]() 中,易得
中,易得![]() ,
,
在![]() 中,
中, ![]() ,所以
,所以![]()
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ) 当![]() 为
为![]() 的三等分点(靠近
的三等分点(靠近![]() )时,
)时, ![]() 平面
平面![]() .
.
证明如下:
因为![]() ,
, ![]() ,所以
,所以![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(注:学生不写![]() 平面
平面![]() ,扣1分)
,扣1分)
(Ⅲ) 由(Ⅰ)知![]() 平面
平面![]() ,所以
,所以![]() 为三棱锥
为三棱锥![]() 的高.
的高.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由等体积法得
,由等体积法得![]() ,
,
即![]() ,又
,又![]() ,
,![]() ,
,
所以![]() ,即点
,即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x , x∈(0,2)的值域为A,函数g(x)=log2(x﹣2a)+ ![]() (a<1)的定义域为B.
(a<1)的定义域为B.
(Ⅰ)求集合A,B;
(Ⅱ)若BA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣4x+a+3,g(x)=mx+5﹣2m
(1)当a=﹣3,m=0时,求方程f(x)﹣g(x)=0的解;
(2)若方程f(x)=0在[﹣1,1]上有实数根,求实数a的取值范围;
(3)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
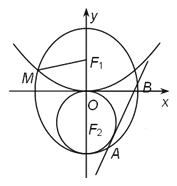
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的上、下焦点,
的上、下焦点, ![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是
是![]() 与
与![]() 在第二象限的交点,且
在第二象限的交点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,
若椭圆![]() 上一点
上一点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少又一次得满分的学生有15名.若后两次均为满分的学生至多有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,x∈R.
,x∈R.
(1)求证:对一切实数x,f(x)=f(1﹣x)恒为定值.
(2)计算:f(﹣6)+f(﹣5)+f(﹣4)+f(﹣3)+…+f(0)+…+f(6)+f(7).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对任意x∈[m,n]均有|f(x)﹣g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的;否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x﹣3a),与f2(x)=loga ![]() (a>0,a≠1),给定区间[a+2,a+3].
(a>0,a≠1),给定区间[a+2,a+3].
(1)若f1(x)与f1(x)在给定区间[a+2,a+3]上都有意义,求a的取值范围;
(2)讨论f1(x)与f1(x)在给定区间[a+2,a+3]上是否是接近的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某企业生产的一批产品中有一、二、三等品及次品共四个等级,1件不同等级产品的利润(单位:元)如表1,从这批产品中随机抽取出1件产品,该件产品为不同等级的概率如表2.
等级 | 一等品 | 二等品 | 三等品 | 次品 |
|
| |
|
|
等级 | 一等品 | 二等品 | 三等品 | 次品 |
利润 | |
|
|
|
表1 表2
若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为![]() 元.
元.
(1) 设随机抽取1件产品的利润为随机变量![]() ,写出
,写出![]() 的分布列并求出
的分布列并求出![]() 的值;
的值;
(2) 从这批产品中随机取出3件产品,求这3件产品的总利润不低于17元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com