
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切求出
相切求出![]() ,再由离心率和
,再由离心率和![]() 关系,可求出椭圆标准方程;
关系,可求出椭圆标准方程;
(2)将直线![]() 与椭圆方程联立,消元整理,由根与系数关系,得到
与椭圆方程联立,消元整理,由根与系数关系,得到![]() 的两个关系式,再从已知条件寻找
的两个关系式,再从已知条件寻找![]() 第三个等量关系,根据已知结合平面图形,可得
第三个等量关系,根据已知结合平面图形,可得![]() 轴,过
轴,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]() 为线段
为线段![]() 的中点,得
的中点,得![]() ,进而有
,进而有![]() ,代入直线
,代入直线![]() 方程,得到
方程,得到![]() 等量关系,求解关于
等量关系,求解关于![]() 方程组,即可求出
方程组,即可求出![]() .
.
(1)依题意,![]() ,
,
因为离心率![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以![]() 的标准方程为
的标准方程为![]() .
.
(2)因为直线![]() 的倾斜角为
的倾斜角为![]() ,
,
且![]() 是以
是以![]() 为顶角的等腰直角三角形,
为顶角的等腰直角三角形,
![]() 在直线
在直线![]() 的右下方,所以
的右下方,所以![]() 轴,
轴,
过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() ,故
,故![]() ,
,
所以![]() ,即
,即![]() ,
,
整理得![]() .①
.①
由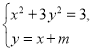 得
得![]() .
.
所以![]() ,解得
,解得![]() ,
,
所以![]() ,②
,②
![]() ,③
,③
由①![]() ②得,
②得,![]() ,④
,④
将④代入②得![]() ,⑤
,⑤
将④⑤代入③得![]() ,解得
,解得![]() .
.
综上,![]() 的值为
的值为![]() .
.



科目:高中数学 来源: 题型:
【题目】如果无穷数列{an}的所有项恰好构成全体正整数的一个排列,则称数列{an}具有性质P.
(Ⅰ)若an![]() (k∈N*),判断数列{an}是否具有性质P,并说明理由,
(k∈N*),判断数列{an}是否具有性质P,并说明理由,
(Ⅱ)若数列{an}具有性质P,求证:{an}中一定存在三项ai,aj,ak(i<j<k)构成公差为奇数的等差数列;
(Ⅲ)若数列{an}具有性质P,则{an}中是否一定存在四项ai,aj,ak,al,(i<j<k<l)构成公差为奇数的等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:给定整数i,如果非空集合满足如下3个条件:
①![]() ;②
;②![]() ;③
;③![]() ,若
,若![]() ,则
,则![]() .
.
则称集合A为“减i集”
(1)![]() 是否为“减0集”?是否为“减1集”?
是否为“减0集”?是否为“减1集”?
(2)证明:不存在“减2集”;
(3)是否存在“减1集”?如果存在,求出所有“减1集”;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
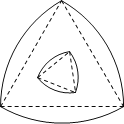
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为______.
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且椭圆上存在一点
,且椭圆上存在一点![]() ,满足
,满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com