
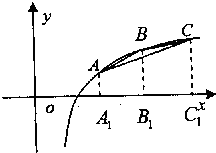 在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).
在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).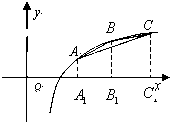 解:(1)∵f(m-1)+f(m+1)=lg(m-1)+lg(m+1)=lg(m2-1),2f(m)=2lgm=lgm2>lg(m2-1),
解:(1)∵f(m-1)+f(m+1)=lg(m-1)+lg(m+1)=lg(m2-1),2f(m)=2lgm=lgm2>lg(m2-1),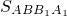 +
+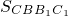 -
-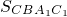
 [lg(m-1)+lgm]+
[lg(m-1)+lgm]+ [lg(m+1)+lgm]-
[lg(m+1)+lgm]- [lg(m-1)+lg(m+1)]×2=
[lg(m-1)+lg(m+1)]×2= lg[
lg[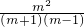 ]=
]= lg(1+
lg(1+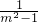 ),
), lg
lg ,
, lg
lg ].
].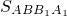 +
+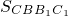 -
-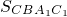 ,化简为
,化简为 lg(1+
lg(1+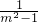 ),再根据m>2时,S=g(m)单调递减求得△ABC的面积S的值域.
),再根据m>2时,S=g(m)单调递减求得△ABC的面积S的值域.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x-y |
| 1-xy |
| 1 |
| 2 |
| 2an | ||
1+
|
| 1 |
| g(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 1-x |
| A、(-∞,+∞)上的减函数 |
| B、(-∞,+∞)上的增函数 |
| C、(-1,1)上的减函数 |
| D、(-1,1)上的增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
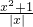 (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题:查看答案和解析>>
科目:高中数学 来源:2011-2012学年辽宁省本溪一中、庄河高中联考高三(上)期末数学试卷(理科)(解析版) 题型:填空题
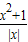 (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题:查看答案和解析>>
科目:高中数学 来源:2012年辽宁省盘锦二高高考数学一模试卷(理科)(解析版) 题型:填空题
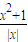 (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com