
已知函数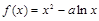 (
(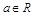 )。
)。
(1)若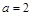 ,求证:
,求证: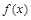 在
在 上是增函数;
上是增函数;
(2)求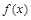 在
在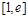 上的最小值。
上的最小值。
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
已知函数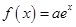 ,
,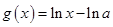 ,其中
,其中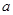 为常数,
为常数,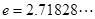 ,函数
,函数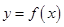 和
和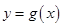 的图像在它们与坐标轴交点处的切线分别为
的图像在它们与坐标轴交点处的切线分别为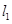 、
、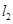 ,且
,且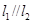 .
.
(1)求常数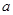 的值及
的值及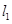 、
、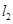 的方程;
的方程;
(2)求证:对于函数 和
和 公共定义域内的任意实数
公共定义域内的任意实数 ,有
,有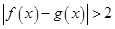 ;
;
(3)若存在 使不等式
使不等式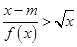 成立,求实数
成立,求实数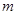 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校内有一块以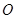 为圆心,
为圆心,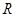 (
(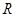 为常数,单位为米)为半径的半圆形(如图)荒地,该校总务处计划对其开发利用,其中弓形
为常数,单位为米)为半径的半圆形(如图)荒地,该校总务处计划对其开发利用,其中弓形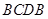 区域(阴影部分)用于种植学校观赏植物,
区域(阴影部分)用于种植学校观赏植物,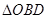 区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.
区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.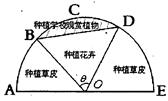
(1)设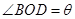 (单位:弧度),用
(单位:弧度),用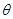 表示弓形
表示弓形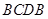 的面积
的面积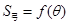 ;
;
(2)如果该校总务处邀请你规划这块土地,如何设计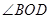 的大小才能使总利润最大?并求出该最大值.
的大小才能使总利润最大?并求出该最大值.
(参考公式:扇形面积公式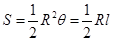 ,
,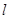 表示扇形的弧长)
表示扇形的弧长)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com