
【题目】下列结论中
①若空间向量![]() ,
,![]() ,则
,则![]() 是
是![]() 的充要条件;
的充要条件;
②若![]() 是
是![]() 的必要不充分条件,则实数
的必要不充分条件,则实数![]() 的取值范围为
的取值范围为![]() ;
;
③已知![]() ,
,![]() 为两个不同平面,
为两个不同平面,![]() ,
,![]() 为两条直线,
为两条直线,![]() ,
,![]() ,
,![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
④已知向量![]() 为平面
为平面![]() 的法向量,
的法向量,![]() 为直线
为直线![]() 的方向向量,则
的方向向量,则![]() 是
是![]() 的充要条件.
的充要条件.
其中正确命题的序号有( )
A.②③B.②④C.②③④D.①②③④
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求椭圆![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
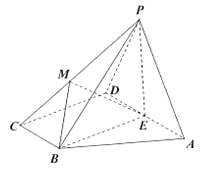
【题目】如图,四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,且
,且![]() ,
,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为等边三角形,
为等边三角形,![]() 是棱
是棱![]() 上的一点,设
上的一点,设![]() (
(![]() 与
与![]() 不重合).
不重合).
(1)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆上任意一点,
为椭圆上任意一点,![]() ,
,![]() 分别为椭圆的左、右焦点,且
分别为椭圆的左、右焦点,且![]() ,
,![]() ,
,![]() 依次成等比数列,其离心率为
依次成等比数列,其离心率为![]() .过点
.过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)在平面直角坐标系![]() 中,若存在与点
中,若存在与点![]() 不同的点
不同的点![]() ,使得
,使得![]() 成立,求点
成立,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计调查数据显示:某企业某种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,从该企业生产的这种产品(数量很大)中抽取100件,测量这100件产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
,从该企业生产的这种产品(数量很大)中抽取100件,测量这100件产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
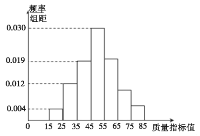
(1)求这100件产品质量指标值落在区间![]() 内的频率;
内的频率;
(2)根据频率分布直方图求平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)若![]() 取这100件产品指标的平均值
取这100件产品指标的平均值![]() ,从这种产品(数量很大)中任取3个,求至少有1个
,从这种产品(数量很大)中任取3个,求至少有1个![]() 落在区间
落在区间![]() 的概率.
的概率.
参考数据:![]() ,若
,若![]() ,则
,则![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一大批产品,其验收方案如下,先做第一次检验:从中任取8件,经检验都为优质品时接受这批产品,若优质品数小于6件则拒收;否则做第二次检验,其做法是从产品中再另任取3件,逐一检验,若检测过程中检测出非优质品就要终止检验且拒收这批产品,否则继续产品检测,且仅当这3件产品都为优质品时接受这批产品.若产品的优质品率为0.9.且各件产品是否为优质品相互独立.
(1)记![]() 为第一次检验的8件产品中优质品的件数,求
为第一次检验的8件产品中优质品的件数,求![]() 的期望与方差;
的期望与方差;
(2)求这批产品被接受的概率;
(3)若第一次检测费用固定为1000元,第二次检测费用为每件产品100元,记![]() 为整个产品检验过程中的总费用,求
为整个产品检验过程中的总费用,求![]() 的分布列.
的分布列.
(附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面![]() 底面ABCD,且
底面ABCD,且![]() ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.
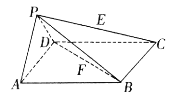
(I)求证:EF//平面PAD;
(II)求三棱锥F-DEC的体积;
(III)在线段CD上是否存在一点G,使得平面![]() 平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com