
【题目】在一次考试中,某班级50名学生的成绩统计如下表,规定75分以下为一般,大于等于75分小于85分为良好,85分及以上为优秀.
分数 | 69 | 73 | 74 | 75 | 77 | 78 | 79 | 80 | 82 | 83 | 85 | 87 | 89 | 93 | 95 | 合计 |
人数 | 2 | 4 | 4 | 2 | 3 | 4 | 6 | 3 | 3 | 4 | 4 | 5 | 2 | 3 | 1 | 50 |
经计算,样本的平均值![]() ,标准差
,标准差![]() .为评判该份试卷质量的好坏,从其中任取一人,记其成绩为X,并根据以下不等式进行评判:
.为评判该份试卷质量的好坏,从其中任取一人,记其成绩为X,并根据以下不等式进行评判:
①![]() ;
;
②![]() ;
;
③![]() .
.
评判规则:若同时满足上述三个不等式,则被评为优秀试卷;若仅满足其中两个不等式,则被评为合格试卷;其他情况,则被评为不合格试卷.
(1)试判断该份试卷被评为哪种等级;
(2)按分层抽样的方式从3个层次的学生中抽出10名学生,再从抽出的10名学生中随机抽出4人进行学习方法交流,用随机变量表示4人中成绩优秀的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,且过点
的焦距为2,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为
为![]() 的左焦点,点
的左焦点,点![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于两点
于两点![]() ,
,![]()
(ⅰ)证明:![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(ⅱ)当![]() 取最小值时,求点
取最小值时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受传统观念的影响,中国家庭教育过程中对子女教育的投入不遗余力,基础教育消费一直是中国家庭教育的重头戏,升学压力的逐渐增大,特别是对于升入重点学校的重视,导致很多家庭教育支出增长较快,下面是某机构随机抽样调查某二线城市2012-2018年的家庭教育支出的折线图.
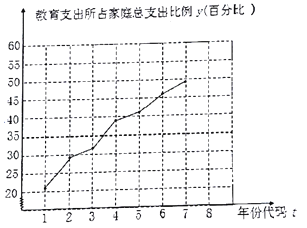
(附:年份代码1-7分别对应的年份是2012-2018)
(1)从图中的折线图看出,可用线性回归模型拟合y与t的关系,请求出相关系数r(精确到0.001),并指出是哪一层次的相关性?(相关系数![]() ,相关性很强;
,相关性很强;![]() ,相关性一般;
,相关性一般;![]() ,相关性较弱).
,相关性较弱).
(2)建立y关于t的回归方程;
(3)若2019年该地区家庭总支出为10万元,预测家庭教育支出约为多少万元?
附注:参考数据:![]() ,
,![]() ,
,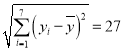 ,
,![]() ,
,![]() .
.
参考公式: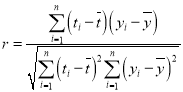 ,回归方程
,回归方程![]() ,
,
其中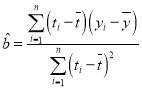 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中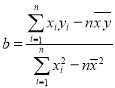 .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龙)、巳(蛇)、午(马)、未(羊)、申(猴)、酉(鸡)、戌(狗)、亥(猪),每一个人的出生年份对应了十二种动物中的一种,即自己的属相.现有印着十二生肖图案的毛绒娃娃各一个,小张同学的属相为马,小李同学的属相为羊,现在这两位同学从这十二个毛绒娃娃中各随机取一个(不放回),则这两位同学都拿到自己属相的毛绒娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每个国家对退休年龄都有不一样的规定,从2018年开始,我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)若从年龄在![]() 的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为
的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,不等式
,不等式![]() 的解集是
的解集是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)不等式组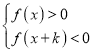 的正整数解只有一个,求实数k取值范围;
的正整数解只有一个,求实数k取值范围;
(3)若对于任意![]() ,不等式
,不等式![]() 恒成立,求t的取值范围.
恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 、
、![]() 在抛物线上,且
在抛物线上,且![]() 、
、![]() 、
、![]() 三点共线.若圆
三点共线.若圆![]() 的直径为
的直径为![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
,![]() ,分别过
,分别过![]() 、
、![]() 两点作抛物线
两点作抛物线![]() 的切线
的切线![]() ,
,![]() ,证明直线
,证明直线![]() ,
,![]() 的交点在定直线上,并求出该直线.
的交点在定直线上,并求出该直线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com