
【题目】设函数![]() ,
,![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,若存在正实数
,若存在正实数![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)对函数求导,对a分类讨论得到导函数的正负进而得到单调性;(2)对a分情况讨论,在不同的范围下,得到函数![]() 的正负,进而去掉绝对值,再构造函数,转化为函数最值问题.
的正负,进而去掉绝对值,再构造函数,转化为函数最值问题.
(1)∵![]() ,(
,(![]() )
)
①若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 为增函数
为增函数
②若![]() 时,则
时,则![]() ,
,![]() ,
,
故![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数
为增函数
(2)①若![]() ,则
,则![]()
由(1)知![]() 在
在![]() 为增函数,又
为增函数,又![]() ,所以
,所以![]() 对
对![]() 恒成立,
恒成立,
则![]()
设![]() ,(
,(![]() ),则
),则![]() 等价于
等价于![]()
![]() ,
,![]() ,
,![]() ,
,
故![]() 在
在![]() 递减,在
递减,在![]() 递增,而
递增,而![]() ,显然当
,显然当![]() ,
,![]() ,
,
故不存在正实数![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,
恒成立,
故![]() 不满足条件
不满足条件
②若![]() ,则
,则![]() ,由(1)知
,由(1)知![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,∵
为增函数,∵![]() ,
,
∴当![]() 时,
时,![]() ,此时
,此时![]()
![]()
∴设![]() ,
,![]() ,此时
,此时![]() 等价于
等价于![]()
![]() ,
,![]()
(i)若![]() ,∵
,∵![]() ∴
∴![]() ,
,![]() 在
在![]() 为增函数,
为增函数,
∵![]() ,∴
,∴![]() ,
,![]()
故不存在正实数![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,
恒成立,
故![]() 不满足条件
不满足条件
(ii)若![]() ,易知
,易知![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,
∵![]() ,∴
,∴![]() ,
,![]() ,故存在正实数
,故存在正实数![]() ,(可取
,(可取![]() )
)
使得对任意![]() 都有
都有![]() 恒成立,故
恒成立,故![]() 满足条件
满足条件


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,如果把它的12条棱延伸为直线,6个面延展为平面,那么在这12条直线与6个平面中:
中,如果把它的12条棱延伸为直线,6个面延展为平面,那么在这12条直线与6个平面中:

(1)与直线![]() 不平行也不相交的直线有哪几条?
不平行也不相交的直线有哪几条?
(2)与直线![]() 平行的平面有哪几个?
平行的平面有哪几个?
(3)与直线![]() 垂直的平面有哪几个?
垂直的平面有哪几个?
(4)与平面![]() 平行的平面有哪几个?
平行的平面有哪几个?
(5)与平面![]() 垂直的平面有哪几个?
垂直的平面有哪几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
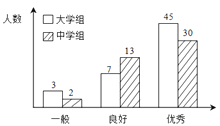
若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95﹪的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注: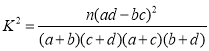 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.005 |
| 2.706 | 3.841 | 7.879 |
(2)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题中p是q的什么条件.(充分不必要条件必要不充分条件,充要条件,既不充分也不必要条件)
(1)p:数a能被6整除,q:数a能被3整除;
(2)![]() ,
,![]() ;
;
(3)![]() 有两个角相等,
有两个角相等,![]() 是正三角形;
是正三角形;
(4)若![]() ,
,![]() ,
,![]() ;
;
(5)![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知国家某5A级大型景区对每日游客数量拥挤等级规定如下表:
游客数量(百人) |
|
|
|
|
拥挤等级 | 优 | 良 | 拥挤 | 严重拥挤 |
该景区对![]() 月份的游客量作出如图的统计数据:
月份的游客量作出如图的统计数据:

(Ⅰ)下面是根据统计数据得到的频率分布表,求![]() ,
,![]() 的值;
的值;
游客数量(百人) |
|
|
|
|
天数 |
| 10 | 4 | 1 |
频率 |
|
|
|
|
(Ⅱ)估计该景区![]() 月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表):
月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表):
(Ⅲ)某人选择在![]() 月
月![]() 日至
日至![]() 月
月![]() 日这
日这![]() 天中任选
天中任选![]() 天到该景区游玩,求他这
天到该景区游玩,求他这![]() 天遇到的游客拥挤等级均为优的概率.
天遇到的游客拥挤等级均为优的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
①双曲线![]() 的渐近线方程为y=±
的渐近线方程为y=±![]() x;
x;
②命题p:“x∈R,sinx+![]() ≥2”是真命题;
≥2”是真命题;
③已知线性回归方程为![]() =3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
=3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=0.2,则P(-1<ξ<0)=0.6;
⑤设![]() ,则
,则![]()
则正确命题的序号为________(写出所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com