
【题目】判断下列命题中p是q的什么条件.(充分不必要条件必要不充分条件,充要条件,既不充分也不必要条件)
(1)p:数a能被6整除,q:数a能被3整除;
(2)![]() ,
,![]() ;
;
(3)![]() 有两个角相等,
有两个角相等,![]() 是正三角形;
是正三角形;
(4)若![]() ,
,![]() ,
,![]() ;
;
(5)![]() ,
,![]() .
.
【答案】(1)p是q的充分不必要条件(2)P是q的充分不必要条件(3)p是q的必要不充分条件(4)p是q的充要条件(5)p是q的既不充分也不必要条件
【解析】
判断两个命题![]() 和
和![]() 是否正确,然后得结论.
是否正确,然后得结论.
解析(1)因为“数a能被6整除”能推出“数a能被3整除”,所以![]() ,
,
但“数a能被3整除”推不出“数a能被6整除”,如![]() ,所以
,所以![]() ,所以p是q的充分不必要条件.
,所以p是q的充分不必要条件.
(2)因为![]() 能推出
能推出![]() ,即
,即![]() ;但当
;但当![]() 时,如
时,如![]() ,推不出
,推不出![]() ,即
,即![]() ,所以P是q的充分不必要条件.
,所以P是q的充分不必要条件.
(3)因为“![]() 有两个角相等”推不出“
有两个角相等”推不出“![]() 是正三角形”,因此
是正三角形”,因此![]() ,但“
,但“![]() 是正三角形”能推出“
是正三角形”能推出“![]() 有两个角相等”,即
有两个角相等”,即![]() ,所以p是q的必要不充分条件.
,所以p是q的必要不充分条件.
(4)若![]() ,则
,则![]() ,即
,即![]() ;若
;若![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() ,所以p是q的充要条件.
,所以p是q的充要条件.
(5)当![]() ,
,![]() 时,
时,![]() 推不出
推不出![]() ,知
,知![]() ,又当
,又当![]() ,
,![]() 时,
时,![]() 推不出
推不出![]() ,知
,知![]() ,所以p是q的既不充分也不必要条件.
,所以p是q的既不充分也不必要条件.


科目:高中数学 来源: 题型:
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: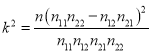 ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: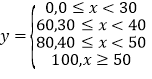 ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
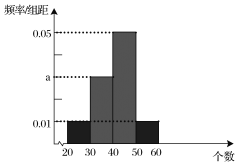
(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某市举行的一次市质检考试中,为了调查考试试题的有效性以及试卷的区分度,该市教研室随机抽取了参加本次质检考试的500名学生的数学考试成绩,并将其统计如下表所示.

根据上表数据统计,可知考试成绩落在![]() 之间的频率为
之间的频率为![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)已知本欢质检中的数学测试成绩![]() ,其中
,其中![]() 近似为样本的平均数,
近似为样本的平均数,![]() 近似为样本方差
近似为样本方差![]() ,若该市有4万考生,试估计数学成绩介于
,若该市有4万考生,试估计数学成绩介于![]() 分的人数;
分的人数;![]() 以各组的区间的中点值代表该组的取值
以各组的区间的中点值代表该组的取值![]() Ⅲ
Ⅲ![]() 现按分层抽样的方法从成绩在
现按分层抽样的方法从成绩在![]() 以及
以及![]() 之间的学生中随机抽取12人,再从这12人中随机抽取4人进行试卷分析,记被抽取的4人中成绩在
之间的学生中随机抽取12人,再从这12人中随机抽取4人进行试卷分析,记被抽取的4人中成绩在![]() 之间的人数为X,求X的分布列以及期望
之间的人数为X,求X的分布列以及期望![]() .
.
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数),以平面直角坐标系的原点为极点,
为参数),以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,试问是否存在实数
两点,试问是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() .沿
.沿![]() 将△
将△![]() 翻折到△
翻折到△![]() ,连接
,连接![]() ,得到如图的五棱锥
,得到如图的五棱锥![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个电路中有A,B,C三个电器元件,每个元件可能正常,也可能失效,把这个电路是否为通路看成是一个随机现象,观察这个电路中各元件是否正常.

(1)写出试验的样本空间;
(2)用集合表示下列事件:M=“恰好两个元件正常”;N=“电路是通路”;T=“电路是断路”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①函数![]() 的单调增区间是
的单调增区间是![]() ;
;
②若函数![]() 定义域为
定义域为![]() 且满足
且满足![]() ,则它的图象关于
,则它的图象关于![]() 轴对称;
轴对称;
③函数![]() 的值域为
的值域为![]() ;
;
④函数![]() 的图象和直线
的图象和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值可能是
的值可能是![]() ;
;
⑤若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .
.
其中正确的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com