
错解:∵x+y=(x+y)![]() ·
·![]() ,∴(x+y)min=
,∴(x+y)min=![]() .
.
错因分析:x+y≥![]() 中等号成立的条件是x=y,
中等号成立的条件是x=y,![]() ≥
≥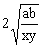 中等号成立的条件是
中等号成立的条件是![]() ,而
,而![]() =1,∴x=2a,y=2b.此时a不一定等于b,故上述解法有误.
=1,∴x=2a,y=2b.此时a不一定等于b,故上述解法有误.
正解一:(消元法)∵![]() =1,∴y=
=1,∴y=![]() 且x>a.
且x>a.
∴x+y=x+![]() =x+
=x+![]() =x+b+
=x+b+![]() =x-a+
=x-a+![]() +a+b≥
+a+b≥![]() +a+b=(
+a+b=(![]() +
+![]() )2.
)2.
正解二:(妙用“1”)x+y=(x+y)(![]() )=a+
)=a+![]() +b≥a+b+
+b≥a+b+![]() =(
=(![]() +
+![]() )2.
)2.
正解三:(三角代换)令![]() =cos2θ,
=cos2θ,![]() =sin2θ,则x+y=asec2θ+bcsc2θ=a(1+tan2θ)+b(1+cot2θ)
=sin2θ,则x+y=asec2θ+bcsc2θ=a(1+tan2θ)+b(1+cot2θ)
=a+b+atan2θ+bcot2θ≥a+b+![]() =(
=(![]() )2.
)2.
上述三种解法均可得出当且仅当x=![]() +a,y=
+a,y=![]() +b时取等号,故(x+y)min=(
+b时取等号,故(x+y)min=(![]() )2.
)2.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com