
【题目】定义向量 ![]() =(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为 ![]() =(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.
=(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.
(1)设g(x)=3sin(x+ ![]() )+4sinx,求证:g(x)∈S;
)+4sinx,求证:g(x)∈S;
(2)已知h(x)=cos(x+α)+2cosx,且h(x)∈S,求其“相伴向量”的模;
(3)已知M(a,b)(b≠0)为圆C:(x﹣2)2+y2=1上一点,向量 ![]() 的“相伴函数”f(x)在x=x0处取得最大值.当点M在圆C上运动时,求tan2x0的取值范围.
的“相伴函数”f(x)在x=x0处取得最大值.当点M在圆C上运动时,求tan2x0的取值范围.
【答案】
(1)解:g(x)=3sin(x+ ![]() )+4sinx=4sinx+3cosx,
)+4sinx=4sinx+3cosx,
其‘相伴向量’ ![]() =(4,3),g(x)∈S
=(4,3),g(x)∈S
(2)解:h(x)=cos(x+α)+2cosx
=(cosxcosα﹣sinxsinα)+2cosx
=﹣sinαsinx+(cosα+2)cosx
∴函数h(x)的‘相伴向量’ ![]() =(﹣sinα,cosα+2).
=(﹣sinα,cosα+2).
则| ![]() |=
|= ![]() =
= ![]()
(3)解: ![]() 的‘相伴函数’f(x)=asinx+bcosx=
的‘相伴函数’f(x)=asinx+bcosx= ![]() sin(x+φ),
sin(x+φ),
其中cosφ= ![]() ,sinφ=
,sinφ= ![]() .
.
当x+φ=2kπ+ ![]() ,k∈Z时,f(x)取到最大值,故x0=2kπ+
,k∈Z时,f(x)取到最大值,故x0=2kπ+ ![]() ﹣φ,k∈Z.
﹣φ,k∈Z.
∴tanx0=tan(2kπ+ ![]() ﹣φ)=cotφ=
﹣φ)=cotφ= ![]() ,
,
tan2x0= ![]() =
= ![]() =
= ![]() .
.
![]() 为直线OM的斜率,由几何意义知:
为直线OM的斜率,由几何意义知: ![]() ∈[﹣
∈[﹣ ![]() ,0)∪(0,
,0)∪(0, ![]() ].
].
令m= ![]() ,则tan2x0=
,则tan2x0= ![]() ,m∈[﹣
,m∈[﹣ ![]() ,0)∪(0,
,0)∪(0, ![]() }.
}.
当﹣ ![]() ≤m<0时,函数tan2x0=
≤m<0时,函数tan2x0= ![]() 单调递减,∴0<tan2x0≤
单调递减,∴0<tan2x0≤ ![]() ;
;
当0<m≤ ![]() 时,函数tan2x0=
时,函数tan2x0= ![]() 单调递减,∴﹣
单调递减,∴﹣ ![]() ≤tan2x0<0.
≤tan2x0<0.
综上所述,tan2x0∈[﹣ ![]() ,0)∪(0,
,0)∪(0, ![]() ].
].
【解析】(1)先利用诱导公式对其化简,再结合定义即可得到证明;(2)先根据定义求出其相伴向量,再代入模长计算公式即可;(3)先根据定义得到函数f(x)取得最大值时对应的自变量x0;再结合几何意义求出 ![]() 的范围,最后利用二倍角的正切公式即可得到结论.
的范围,最后利用二倍角的正切公式即可得到结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AD=1,AB=2,点E是C1D1的中点.
(1)求证:DE⊥平面BCE;
(2)求二面角A﹣EB﹣C的大小.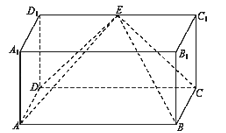
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0,求分别满足下列条件的a,b的值.
(1)直线l1过点(﹣3,﹣1),且l1⊥l2;
(2)l1∥l2 , 且坐标原点到l1与l2的距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() , 其中左焦点F(﹣2,0).
, 其中左焦点F(﹣2,0).
(1)求椭圆C的方程;
(2)若直线y=x+m与椭圆C交于不同的两点A,B,且线段的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为2正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个判断:
①AC⊥BD
②AB与平面BCD所成60°角
③△ABC是等边三角形
④若A、B、C、D四点在同一个球面上,则该球的表面积为8π
其中正确判断的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是绵阳市某小区100户居民2014年平均用水量(单位:t)的频率分布直方图,则该小区2014年的月平均用水量的众数,中位数的估计值分别是( ) 
A.2,2.5
B.2,2.02
C.2.25,2.5
D.2.25,2.02
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的顶点与焦点分别是椭圆 ![]() =1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com