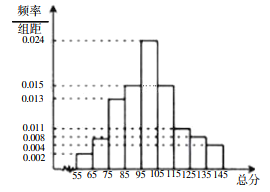
[题目]从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本.分别统计出这些试卷总分.由总分得到如下的频率分别直方图.(1)求这100份数学试卷成绩的中位数,(2)从总分在和的试卷中随机抽取2份试卷.求抽取的2份试卷中至少有一份总分少于65分的概率. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分别直方图.

（1）求这100份数学试卷成绩的中位数；

（2）从总分在和的试卷中随机抽取2份试卷，求抽取的2份试卷中至少有一份总分少于65分的概率.

【答案】（1）100；（2）.

【解析】

（1）通过左边起，频率和为的位置即为中位数的位置.的试卷有份和的试卷有份，利用列举法求得基本事件的总数，从中得到至少有一份总分少于的事件的个数，由此计算得概率.

（1）记这100份数学试卷成绩的中位数为

则

解得：,所以，中位数为100.

（2）总分在共有（份），记为

总分在的试卷共有（份），记为

则从上述6份试卷中随机抽取2份的抽取结果为：，，，，，

，，，，

，，，

，，

，

共计15种结果，且每个结果是等可能的，

至少有一份总分少于65分的有：，，，，，，，，，共计9种结果，

所以抽取的2份至少有一份总分少于65分的概率.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，直线的参数方程为（为参数）.在以原点为极点，轴正半轴为极轴的极坐标系中，曲线的极坐标方程为.

（1）求直线的极坐标方程和曲线的直角坐标方程；

（2）若直线与曲线交于两点，求.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】将一个骰子连续抛掷三次，它落地时向上的点数能组成成等差数列的概率为( )

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

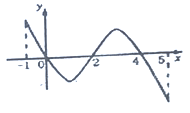
【题目】已知函数的定义域为，部分对应值如下表，的导函数的图象如图所示，给出关于的下列命题：

①函数在处取得极小值;

②函数在是减函数，在是增函数；

③当时，函数有4个零点；

④如果当时，的最大值是2，那么的最小值为0.

其中所有的正确命题是__________(写出正确命题的序号).

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，△ABC和△BCD所在平面互相垂直，且AB=BC=BD=2．∠ABC=∠DBC=120°，E、F分别为AC、DC的中点．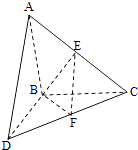

（1）求证：EF⊥BC；
（2）求二面角E﹣BF﹣C的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（题文）已知函数

（I）当时，求函数的单调区间；

（II）当时，若对于区间上的任意两个不相等的实数，都有成立，求实数的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某湿地公园内有一条河，现打算建一座桥将河两岸的路连接起来，剖面设计图纸如下：

其中，点为轴上关于原点对称的两点，曲线段是桥的主体，为桥顶，且曲线段在图纸上的图形对应函数的解析式为，曲线段均为开口向上的抛物线段，且分别为两抛物线的顶点，设计时要求：保持两曲线在各衔接处（）的切线的斜率相等.

（1）求曲线段在图纸上对应函数的解析式,并写出定义域；

（2）车辆从经倒爬坡，定义车辆上桥过程中某点所需要的爬坡能力为：（该点与桥顶间的水平距离）（设计图纸上该点处的切线的斜率），其中的单位：米.若该景区可提供三种类型的观光车:①游客踏乘；②蓄电池动力；③内燃机动力.它们的爬坡能力分别为米,米,米,又已知图纸上一个单位长度表示实际长度米,试问三种类型的观光车是否都可以顺利过桥?