
【题目】设函数![]()
![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 的极大值点为
的极大值点为![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)答案见解析;(Ⅱ)证明见解析.
【解析】分析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() ,据此分类讨论可得:当
,据此分类讨论可得:当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递增;当
单调递增;当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(Ⅱ)由(Ⅰ)知![]() ,原问题等价于证明
,原问题等价于证明![]() .构造函数
.构造函数![]()
![]() ,结合导函数的特征再次构造函数
,结合导函数的特征再次构造函数![]() ,结合函数的性质即可证得题中的结论.
,结合函数的性质即可证得题中的结论.
详解:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则函数
,则函数![]() 在区间
在区间![]() 单调递增;
单调递增;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() .
.
所以,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 单调递减.
单调递减.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递增;
单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(Ⅱ)由(Ⅰ)知![]() 且
且![]() 时,解得
时,解得![]() .
.![]() ,
,
要证![]() ,即证
,即证![]() ,即证:
,即证:![]() .
.
令![]()
![]() ,则
,则![]()
![]() .
.
令![]() ,易见函数
,易见函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
而![]() ,
,![]() ,
,
所以在区间![]() 上存在唯一的实数
上存在唯一的实数![]() ,使得
,使得![]() ,
,
即![]() ,且
,且![]() 时
时![]() ,
,![]() 时
时![]() .
.
故![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
∴![]()
![]() .
.
又![]() ,∴
,∴![]()
![]() .
.
∴![]() 成立,即
成立,即![]() 成立.
成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将6名党员干部分配到4个贫困村驻村扶贫,每个贫困村至少分配1名党员干部,则不同的分配方案共有( )
A.2640种B.4800种C.1560种D.7200种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 件次品和
件次品和![]() 件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出
件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时检测结束.
件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用![]() 元,设
元,设![]() 表示直到检测出
表示直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时所需要的检测费用(单位:元),求
件正品时所需要的检测费用(单位:元),求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人投篮的命中率各不相同,其中乙的命中率是甲的2倍,丙的命中率等于甲与乙的命中率之和.若甲与乙各投篮一次,每人投篮相互独立,则他们都命中的概率为0.18.
(1)求甲、乙、丙三人投篮的命中率;
(2)现要求甲、乙、丙三人各投篮一次,假设每人投篮相互独立,记三人命中总次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,已知圆
,已知圆![]() 将椭圆
将椭圆![]() 的长轴三等分,椭圆
的长轴三等分,椭圆![]() 右焦点到右准线的距离为
右焦点到右准线的距离为![]() ,椭圆
,椭圆![]() 的下顶点为
的下顶点为![]() ,过坐标原点
,过坐标原点![]() 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线![]() 与圆
与圆![]() 相交于点
相交于点![]() 、
、![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 相交于另一个交点为点
相交于另一个交点为点![]() 、
、![]() .
.
①求证:直线![]() 经过一定点;
经过一定点;
②试问:是否存在以![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() ,使得直线
,使得直线![]() 和直线
和直线![]() 都与圆
都与圆![]() 相交?若存在,请求出实数
相交?若存在,请求出实数![]() 的范围;若不存在,请说明理由。
的范围;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与顶点
与顶点![]() 的轨迹交于
的轨迹交于![]() 两点,当线段
两点,当线段![]() 的中点
的中点![]() 落在直线
落在直线![]() 上时,试问:线段
上时,试问:线段![]() 的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() ,
,![]() .给出下列四个结论:
.给出下列四个结论:
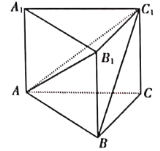
①四棱锥![]() 为阳马;
为阳马;
②直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ;
;
③当![]() 时,异面直线
时,异面直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;
;
④当三棱锥![]() 体积最大时,四棱锥
体积最大时,四棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若一个函数存在极大值,且该极大值为负数,则称这个函数为“![]() 函数”.
函数”.
(1)判断函数![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若函数![]() 是“
是“![]() 函数”,求实数
函数”,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,
,![]() ,
,![]() 、
、![]() ,求证:当
,求证:当![]() ,且
,且![]() 时,函数
时,函数![]() 是“
是“![]() 函数”.
函数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com