
【题目】已知![]() 件次品和
件次品和![]() 件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出
件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时检测结束.
件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用![]() 元,设
元,设![]() 表示直到检测出
表示直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时所需要的检测费用(单位:元),求
件正品时所需要的检测费用(单位:元),求![]() 的分布列.
的分布列.
科目:高中数学 来源: 题型:
【题目】1970年4月24日,我国发射了自己的第一颗人造地球卫星“东方红一号”,从此我国开始了人造卫星的新篇章.人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为![]() ,
,![]() ,下列结论正确的是( )
,下列结论正确的是( )
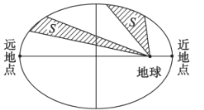
A.卫星向径的取值范围是![]()
B.卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间
C.卫星向径的最小值与最大值的比值越大,椭圆轨道越扁
D.卫星运行速度在近地点时最大,在远地点时最小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国全面二孩政策已于2016年1月1日起正式实施.国家统计局发布的数据显示,从2012年到2017年,中国的人口自然增长率变化始终不大,在5‰上下波动(如图).

为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何,统计部门按年龄分为9组,每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数,得到下表:
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)设每个年龄区间的中间值为![]() ,有意愿数为
,有意愿数为![]() ,求样本数据的线性回归直线方程,并求该模型的相关系数
,求样本数据的线性回归直线方程,并求该模型的相关系数![]() (结果保留两位小数);
(结果保留两位小数);
(2)从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
(参考数据和公式: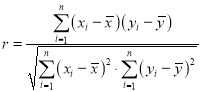 ,
,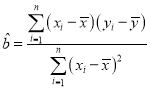 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术,通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量,记一天中从甲地去乙地的旅客人数不超过900的概率为p0.则p0的值为( ).
(参考数据:若X~N(μ,σ2),有P(μ-σ<X≤μ+σ)=0.682 6,P(μ-2σ<X≤μ+2σ)=0.954 4,P(μ-3σ<X≤μ+3σ)=0.997 4.
A.0.954 4B.0.682 6
C.0.997 4D.0.977 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 的两顶点坐标
的两顶点坐标![]() ,
,![]() ,圆
,圆![]() 是
是![]() 的内切圆,在边
的内切圆,在边![]() ,
,![]() ,
,![]() 上的切点分别为
上的切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
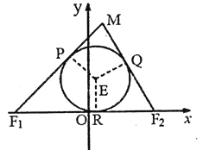
(Ⅰ)求证:![]() 为定值,并求出动点
为定值,并求出动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过![]() 的斜率不为零直线交曲线
的斜率不为零直线交曲线![]() 于
于![]() 、
、![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com