
【题目】已知函数![]() ,其中为自然对数的底数.
,其中为自然对数的底数.
(1)求函数![]() 的极值点;
的极值点;
(2)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,无极值点;当
时,无极值点;当![]() 时,极值点为
时,极值点为![]() ;当
;当![]() 且
且![]() 时,极值点为
时,极值点为![]() 和
和![]() ;(2)
;(2)![]() .
.
【解析】
(1)先求出函数的导数![]() ,讨论
,讨论![]() 、
、![]() 、
、![]() 且
且![]() 即可求出函数的极值点;
即可求出函数的极值点;
(2)由题意可将![]() ,
,![]() 恒成立转化为
恒成立转化为![]() 时,
时,![]() 恒成立,然后构造函数
恒成立,然后构造函数![]() ,分
,分![]() ,
,![]() 与两种情况讨论,分别用导数的方法研究其在
与两种情况讨论,分别用导数的方法研究其在![]() 上的单调性和值域,即可筛选出符合题意的
上的单调性和值域,即可筛选出符合题意的![]() 的取值范围.
的取值范围.
(1)![]() ,
,
当![]() 时,
时,![]() ,故无极值点;
,故无极值点;
当![]() 时,函数
时,函数![]() 只有一个极值点,极值点为
只有一个极值点,极值点为![]() ;
;
当![]() 且
且![]() 时,函数
时,函数![]() 有两个极值点,分别为
有两个极值点,分别为![]() 和
和![]() .
.
(2)![]() ,依题意,当
,依题意,当![]() 时,
时,![]() ,
,
即当![]() 时,
时,![]() .
.
设![]() ,则
,则![]() .
.
设![]() ,则
,则![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,从而
,从而![]() (当且仅当
(当且仅当![]() 时,等号成立),
时,等号成立),
![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() 当
当![]() 时,
时,![]() ,从而当
,从而当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
从而当![]() 时,
时,![]() ,即
,即![]() ,
,
于是当![]() 时,
时,![]() .
.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,![]() .
.
故当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() 当
当![]() 时,
时,![]() ,从而当
,从而当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
从而当![]() 时,
时,![]() ,即
,即![]() ,
,
于是当![]() 时,
时,![]() ,不符合题意.
,不符合题意.
综上所述:实数![]() 的取值范围为
的取值范围为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.设有一个回归方程![]() ,变量x增加1个单位时,y平均减少5个单位
,变量x增加1个单位时,y平均减少5个单位
C.线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),则P(ξ>1)=0.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的顶点与焦点分别是椭圆![]() 的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国工业经济发展迅速,工业增加值连年攀升,某研究机构统计了近十年(从2008年到2017年)的工业增加值(万亿元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工业增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依据表格数据,得到下面的散点图及一些统计量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
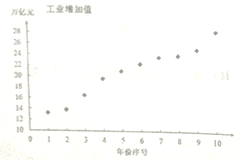
(1)根据散点图和表中数据,此研究机构对工业增加值![]() (万亿元)与年份序号
(万亿元)与年份序号![]() 的回归方程类型进行了拟合实验,研究人员甲采用函数
的回归方程类型进行了拟合实验,研究人员甲采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员乙采用函数
;研究人员乙采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员丙采用线性函数
;研究人员丙采用线性函数![]() ,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数
,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数![]() 与拟合指数
与拟合指数![]() 满足关系
满足关系![]() ).
).
(2)根据(1)的判断结果及统计值,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)预测到哪一年的工业增加值能突破30万亿元大关.
附:样本
![]() 的相关系数
的相关系数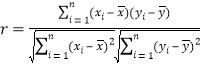 ,
,
![]() ,
,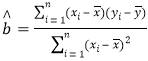 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为
分别为![]() 的左、右顶点,
的左、右顶点,![]() 是
是![]() 上异于
上异于![]() 的动点,
的动点,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 的方程;
的方程;
(2)证明:直线![]() 与直线
与直线![]() 的斜率乘积为定值;
的斜率乘积为定值;
(3)设直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() 两点,以
两点,以![]() 为直径作圆,当圆的面积最小时,求该圆的方程.
为直径作圆,当圆的面积最小时,求该圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级的全体学生平均分成![]() 个小组,且每个小组均有
个小组,且每个小组均有![]() 名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的
名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的![]() 名学生中至少有一名男生的概率为
名学生中至少有一名男生的概率为![]() ,则( )
,则( )
A.该班级共有![]() 名学生
名学生
B.第一小组的男生甲被抽去参加社区服务的概率为![]()
C.抽取的![]() 名学生中男女生数量相同的概率是
名学生中男女生数量相同的概率是![]()
D.设抽取的![]() 名学生中女生数量为
名学生中女生数量为![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为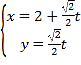 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com