
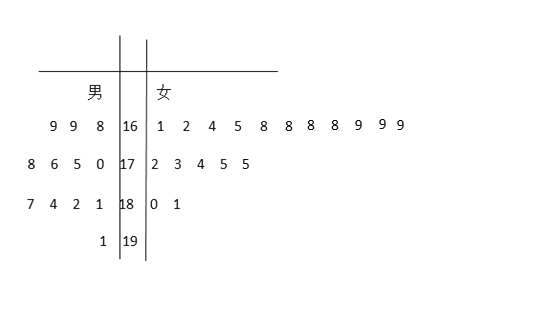
【题目】第24届冬季奥林匹克运动会将于2022年在北京-张家口举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高变成如右所示的茎叶图(单位: ![]() ):若身高在
):若身高在![]() 以上(包括
以上(包括![]() )定义为“高个子”,身高在
)定义为“高个子”,身高在![]() 以下(不包括
以下(不包括![]() )定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(1)如果分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
【答案】(1)![]() (2)见解析,1
(2)见解析,1
【解析】
(1)先根据分层抽样确定5人中“高个子”和“非高个子”人数,再先求对立事件(都不是“高个子”)概率,最后根据对立事件概率公式求结果;
(2)先确定随机变量,再分别求对应概率,写出分布列,最后根据数学期望公式得结果.
解:(1)根据茎叶图,有“高个子”12人,“非高个子”18人用分层抽样的方法,每个人被抽中的概率是![]() ,所以选中的“高个子”有
,所以选中的“高个子”有![]() 人,“非高个子”有
人,“非高个子”有![]() 人.用事件
人.用事件![]() 表示“至少有一名高个子”被选中”,则它的对立事件
表示“至少有一名高个子”被选中”,则它的对立事件![]() 表示“没有一名“高个子”被选中”,则
表示“没有一名“高个子”被选中”,则![]() ,因此,至少有一人是“高个子”的概率是
,因此,至少有一人是“高个子”的概率是![]() .
.
(2)依题意,![]() 的取值为0,1,2,3.
的取值为0,1,2,3.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
因此,![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,平面CDEF⊥平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,ED⊥CD,AB=3EF=3,ED=a,AD![]() .
.
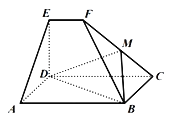
(1)求证:AD⊥BF;
(2)若线段CF上存在一点M,满足AE∥平面BDM,求![]() 的值;
的值;
(3)若a=1,求二面角D﹣BC﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,点
两点,点![]() 满足
满足![]() .
.
(1)当![]() 的倾斜角为
的倾斜角为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为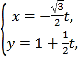 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时至21世纪.环境污染已经成为世界各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开小车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷6枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于4,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的分布列;
(2)由条件概率我们可以得到概率论中一个很重要公式——全概率公式.其特殊情况如下:如果事件![]() 相互对立并且
相互对立并且![]() ,则对任一事件B有
,则对任一事件B有![]() .设
.设![]() 表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
①用![]() 表示
表示![]() ;
;
②王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com