
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD-A1B1C1D1中,AB![]() CD,AB1⊥BC,且AA1=AB.求证:
CD,AB1⊥BC,且AA1=AB.求证:
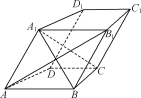
(1)AB![]() 平面D1DCC1;
平面D1DCC1;
(2)AB1⊥平面A1BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A.把![]() 上各点的横坐标变为原来的
上各点的横坐标变为原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B.把![]() 上各点的横坐标变为原来的
上各点的横坐标变为原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C.把![]() 向左平移
向左平移![]() 个单位长度,再把得到的曲线上各点的横坐标变为原来的
个单位长度,再把得到的曲线上各点的横坐标变为原来的![]() 倍.纵坐标不变,得到曲线
倍.纵坐标不变,得到曲线![]()
D.把![]() 向左平移
向左平移![]() 个单位长度,再把得到的曲线上各点的横坐标变为原来的
个单位长度,再把得到的曲线上各点的横坐标变为原来的![]() 倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线C的参数方程为![]() 为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为
为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为![]() .
.
(1)写出曲线C的极坐标方程以及曲线D的直角坐标方程;
(2)若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线l与曲线C交于M,N两点,弦MN的中点为P,求
的直线l与曲线C交于M,N两点,弦MN的中点为P,求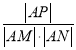 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第24届冬季奥林匹克运动会将于2022年在北京-张家口举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高变成如右所示的茎叶图(单位: ![]() ):若身高在
):若身高在![]() 以上(包括
以上(包括![]() )定义为“高个子”,身高在
)定义为“高个子”,身高在![]() 以下(不包括
以下(不包括![]() )定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
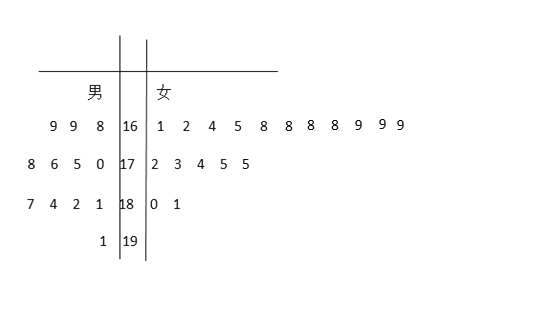
(1)如果分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com