光线自点M(2,3)射到N(1,0)后被x轴反射,则反射光线所在的直线与圆C:x2+(y-4)2=1( )
A.相离
B.相切
C.相交且过圆心
D.相交但不过圆心
【答案】
分析:由点M(2,3)关于x轴对称点是(2,-3),知反射光线过(1,0)和(2,-3);由此能够求出反射光线的方程.由圆x
2+(y-4)
2=1,能求出圆心和半径;再由圆心(0,4)到直线3x+y-3=0的距离d与半径的关系能判断反射光线与圆C:x
2+(y-4)
2=1的关系.
解答:解:∵点M(2,3)关于x轴对称点是(2,-3),
∴反射光线过(1,0)和(2,-3),
∴反射光线的方程:
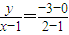
=-3,
即3x+y-3=0.
圆x
2+(y-4)
2=1的圆心是(0,4),半径r=1,
∵圆心(0,4)到直线3x+y-3=0的距离
d=
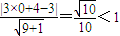
,
∴反射光线3x+y-3=0与圆C:x
2+(y-4)
2=1相交但不过圆心.
故选D.
点评:本题考查直线与圆的位置关系,综合性强,难度大,容易出错.解题时要认真审题,注意点到直线距离公式的灵活运用,合理地进行等价转化.

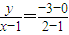 =-3,
=-3,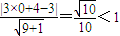 ,
,
