
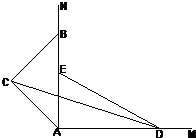
 如图,两射线AM,AN互相垂直,在射线AN上取一点B使AB的长为定值2a,在射线AN的左侧以AB为斜边作一等腰直角三角形ABC.在射线AM,AN上各有一个动点D,E满足△ADE与△ABC的面积之比为3:2,则
如图,两射线AM,AN互相垂直,在射线AN上取一点B使AB的长为定值2a,在射线AN的左侧以AB为斜边作一等腰直角三角形ABC.在射线AM,AN上各有一个动点D,E满足△ADE与△ABC的面积之比为3:2,则 •
•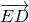 的取值范围为________.
的取值范围为________.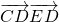 =m2+ma+na.再由△ADE与△ABC的面积之比为3:2,求得n与m的关系.令f(m)=
=m2+ma+na.再由△ADE与△ABC的面积之比为3:2,求得n与m的关系.令f(m)=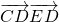 ,利用导数求得函数f(m)取得最小值为 f(m),即可得到
,利用导数求得函数f(m)取得最小值为 f(m),即可得到 •
•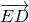 的取值范围.
的取值范围. =(m+a,-a)、
=(m+a,-a)、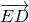 =(m,-n),∴
=(m,-n),∴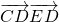 =m2+ma+na.
=m2+ma+na.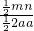 =
= ,∴mn=3a2,∴n=
,∴mn=3a2,∴n=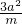 .
.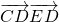 ,则 f(m)=m2+ma+na=m2+ma+
,则 f(m)=m2+ma+na=m2+ma+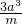 ,
,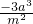 =
=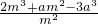 .
.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年天津市河北区高考数学一模试卷(理科)(解析版) 题型:填空题
 )=-
)=- ;
; ,0)对称.
,0)对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com