
【题目】已知平面![]() 有一个公共点,直线
有一个公共点,直线![]() 满足:
满足:![]() ,则直线
,则直线![]() 不可能满足以下哪种关系( )
不可能满足以下哪种关系( )
A.两两平行B.两两异面C.两两垂直D.两两相交
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB = 60m,BC = 80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB= α,矩形区域内的铺设水管的总费用为W.
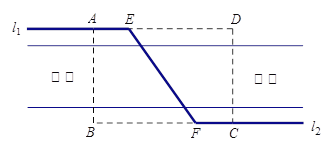
(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数
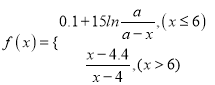
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 的对称中心为坐标原点,则关于函数
的对称中心为坐标原点,则关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的最小正周期为
的最小正周期为![]() ②若
②若![]() 的最大值为2,则
的最大值为2,则![]()
③![]() 在
在![]() 有两个零点 ④
有两个零点 ④![]() 在区间
在区间![]() 上单调
上单调
其中所有正确结论的标号是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率作了调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
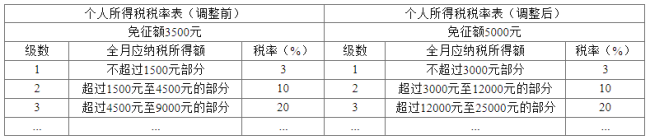
(1)假如小明某月的工资、薪金等税前收入为7500元,请你帮小明算一下调整后小明的实际收入比调整前增加了多少?
(2)某税务部门在小明所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
![]()
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量
的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,求
元的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com