
【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
直线![]() 与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一点,若过点![]() 的直线
的直线![]() 与椭圆C相交于不同的两点S和T,
与椭圆C相交于不同的两点S和T,
满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(1)设椭圆的方程,用待定系数法求出![]() 的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式![]() :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论..
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论..
试题解析:(Ⅰ)由题意,以椭圆![]() 的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为
的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为![]() ,
,
∴圆心到直线![]() 的距离
的距离![]() (*)
(*)
∵椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
∴![]() ,
,![]() , 代入(*)式得
, 代入(*)式得![]() ,∴
,∴![]() ,
,
故所求椭圆方程为![]()
(Ⅱ)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程为
方程为![]() ,设
,设![]() ,
,
将直线方程代入椭圆方程得:![]() ,
,
∴![]() ,∴
,∴![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
由![]() ,
,
当![]() ,直线
,直线![]() 为
为![]() 轴,
轴, ![]() 点在椭圆上适合题意;
点在椭圆上适合题意;
当![]() ,得
,得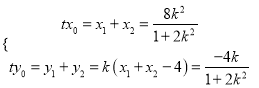 ∴
∴![]()
![]()
![]() .
.
将上式代入椭圆方程得:![]() ,
,
整理得:![]() ,由
,由![]() 知,
知,![]() ,所以
,所以![]() ,
,
综上可得![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某超市在元旦期间开展优惠酬宾活动,凡购物满100元可抽奖一次,满200元可抽奖两次…依此类推.抽奖箱中有7个白球和3个红球,其中3个红球上分别标有10元,10元,20元字样.每次抽奖要从抽奖箱中有放回地任摸一个球,若摸到红球,根据球上标注金额奖励现金;若摸到白球,没有任何奖励.
(Ⅰ)一次抽奖中,已知摸中了红球,求获得20元奖励的概率;
(Ⅱ)小明有两次抽奖机会,用![]() 表示他两次抽奖获得的现金总额,写出
表示他两次抽奖获得的现金总额,写出![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的公比
的公比![]() ,前n项和为
,前n项和为![]() .若
.若![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(1)求![]() ;
;
(2)数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的前2019项和;
的前2019项和;
(3)设![]() ,问数列
,问数列![]() 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为了让高一学生更有效率地利用周六的时间,在高一新生第一次摸底考试后采取周六到校自主学习,同时由班主任老师值班,家长轮流值班.一个月后进行了第一次月考,高一数学教研组通过系统抽样抽取了![]() 名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:
名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:

(1)请画出这次调查得到的![]() 列联表;并判定能否在犯错误概率不超过
列联表;并判定能否在犯错误概率不超过![]() 的前提下认为周六到校自习对提高学生成绩有效?
的前提下认为周六到校自习对提高学生成绩有效?
(2)从这组学生摸底考试中数学优良成绩中和第一次月考的数学非优良成绩中,按分层抽样随机抽取![]() 个成绩,再从这
个成绩,再从这![]() 个成绩中随机抽取
个成绩中随机抽取![]() 个,求这
个,求这![]() 个成绩来自同一次考试的概率.
个成绩来自同一次考试的概率.
下面是临界值表供参考:

(参考公式:  ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)若销售金额(单位:万元)不低于平均值![]() 的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com