
����Ŀ��Ϊ�˱���ij��ҩƷ����Ҫҩ���ɷ��ڹ���ҩƷ�ල�����ֹ涨��ֵ��Χ�ڣ�ij��ҩ���ڸ�ҩƷ�����������У�����Ա��һ���а��չ涨ÿ���2Сʱ�Ը�ҩƷ���м�⣬ÿ����4��:ÿ�μ���ɼ���Ա�Ӹ�ҩƷ�������������ȡ20����Ʒ���м�⣬��������Ҫҩ���ɷֺ���(��λ:mg).�����������飬������Ϊ����ҩƷ����������״̬�������IJ�Ʒ������Ҫҩ���ɷֺ���������̬�ֲ�![]() .
.
��1����������״̬��������![]() ��ʾij�γ�ȡ��20����Ʒ������Ҫҩ���ɷֺ�����
��ʾij�γ�ȡ��20����Ʒ������Ҫҩ���ɷֺ�����![]() ֮���ҩƷ��������
֮���ҩƷ��������![]() (��ȷ��0.001)��
(��ȷ��0.001)��![]() ����ѧ������
����ѧ������
��2����һ�����Ĵμ���У������һ�γ�������Ҫҩ���ɷֺ�����![]() ֮���ҩƷ������Ϊ��������������һ����������̿��ܳ������쳣�������Ա��ε��������̽��м�飻�����һ���У����������μ���������Ҫҩ���ɷֺ�����
֮���ҩƷ������Ϊ��������������һ����������̿��ܳ������쳣�������Ա��ε��������̽��м�飻�����һ���У����������μ���������Ҫҩ���ɷֺ�����![]() ֮���ҩƷ������ֹͣ��������ԭ���Ͻ��м��.
֮���ҩƷ������ֹͣ��������ԭ���Ͻ��м��.
�������Ǽ���Ա��ijһ�γ�ȡ��20��ҩƷ����Ҫҩ���ɷֺ���:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
�������![]() ��
��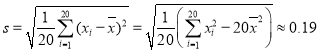 .����
.����![]() Ϊ��ȡ�ĵ�
Ϊ��ȡ�ĵ�![]() ��ҩƷ����Ҫҩ���ɷֺ�����
��ҩƷ����Ҫҩ���ɷֺ�����![]() .������ƽ����
.������ƽ����![]() ��Ϊ
��Ϊ![]() �Ĺ���ֵ
�Ĺ���ֵ![]() ������������
������������![]() ��Ϊ
��Ϊ![]() �Ĺ���ֵ
�Ĺ���ֵ![]() �����ù���ֵ�ж��Ƿ���Ա��ε��������̽��м��?
�����ù���ֵ�ж��Ƿ���Ա��ε��������̽��м��?
����ȷ��һ������ֹͣ��������ԭ���Ͻ��м��ĸ���(��ȷ��0.001).��:���������Z������̬�ֲ�![]() ����
����![]() ��
��
![]() .
.
���𰸡���1��![]() ��
��![]() ��2������Ҫ����0.007
��2������Ҫ����0.007
��������
��1��������֪�����Ҫҩ���ɷֺ�����![]() ֮��ĸ���Ϊ0.0026����
֮��ĸ���Ϊ0.0026����
![]() �����ݶ����ظ�ʵ����ʹ�ϵ���Լ����ηֲ���������������⣻
�����ݶ����ظ�ʵ����ʹ�ϵ���Լ����ηֲ���������������⣻
��2�����![]() ��
��![]() ���������
���������![]() ��ֵ������������û�ж��ڷ�Χ�ڣ�������Ҫ��Ա��ε��������̽��м�飻
��ֵ������������û�ж��ڷ�Χ�ڣ�������Ҫ��Ա��ε��������̽��м�飻
��3���������һ�μ���У�������Ҫ�Ա��ε��������̽��м�����ĸ��ʣ��������¼����ʹ�ϵ��������������γ�������Ҫҩ���ɷֺ�����![]() ֮���ҩƷ���������.
֮���ҩƷ���������.
��1����ȡ��һ��ҩƷ����Ҫҩ���ɷֺ�����
![]() ֮�ڵĸ���Ϊ0.9974��
֮�ڵĸ���Ϊ0.9974��
�Ӷ���Ҫҩ���ɷֺ�����![]()
֮��ĸ���Ϊ0.0026����![]() .
.
���![]() ��
��
![]() ����ѧ����Ϊ
����ѧ����Ϊ![]() ��
��
��2������![]() ��
��![]() ����
����![]() �Ĺ���ֵΪ
�Ĺ���ֵΪ
![]() ��
��![]() �Ĺ���ֵΪ
�Ĺ���ֵΪ![]() ��
��
���������ݿ��Կ�����һ��ҩƷ����Ҫҩ���ɷ�(9.22)������![]() ֮�⣬�����Ա��ε��������̽��м��.
֮�⣬�����Ա��ε��������̽��м��.
��������һ�μ���У�������Ҫ�Ա��ε��������̽��м����Ϊ�¼�![]() ����
����![]() ��
��
�����һ���У���ֹͣ��������ԭ���Ͻ��м�⣬
����һ����Ĵμ���У����������γ�������Ҫҩ���ɷֺ���
��![]() ֮���ҩƷ���ʸ���Ϊ
֮���ҩƷ���ʸ���Ϊ![]() .
.
��ȷ��һ�������ԭ���Ͻ��м��ĸ���Ϊ0.007.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Բ![]() ��������M��0��m����ֱ�߽�x���ڵ�N������ԲC��A��P������P�ڵ�һ���ޣ�N����Բ�ڣ�����M���߶�PN���е㣬��P����x��ĶԳƵ�ΪQ���ӳ�QM��C�ڵ�B����ֱ��PM��QM��б�ʷֱ�Ϊk1��k2��
��������M��0��m����ֱ�߽�x���ڵ�N������ԲC��A��P������P�ڵ�һ���ޣ�N����Բ�ڣ�����M���߶�PN���е㣬��P����x��ĶԳƵ�ΪQ���ӳ�QM��C�ڵ�B����ֱ��PM��QM��б�ʷֱ�Ϊk1��k2��
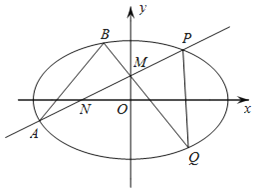
��1����![]() ʱ����k2��ֵ��
ʱ����k2��ֵ��
��2����![]() ʱ����ֱ��ABб�ʵ���Сֵ��
ʱ����ֱ��ABб�ʵ���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ԲO��ֱ��AB��6��CΪԲ����һ�㣬BC��3��ƽ��PAC��ֱԲO����ƽ�棬ֱ��PC��ԲO����ƽ�����ɽ�Ϊ60�㣬PA��PC��
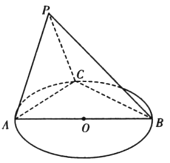
��1��֤����AP��ƽ��PBC
��2��������P��ABһC������ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��ʾ������ʵ��
��ʾ������ʵ��![]() ���������������
���������������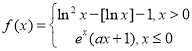 ��������
��������![]() �ķ���
�ķ���![]() ����ֻ��5���⣬��ʵ��
����ֻ��5���⣬��ʵ��![]() ��ȡֵ��ΧΪ�� ��
��ȡֵ��ΧΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Cn��x2��2nx+y2=0����n=1��2������.�ӵ�P����1��0��������Cn��б��Ϊkn��kn>0��������ln���е�ΪPn��xn��yn��.
(1)������{xn}��{yn}��ͨ�ʽ��
(2)֤����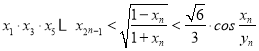 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���飬һ���棬һ���ӣ�һ���š��������ݵij�����Ƭ�������ڡ����������ɡ��ֳ�Ϊ�����ݵ���һ����Ƭ������ȫ���˶�������ʶ����ߣ��������˶����������ݣ�������ȫ��������������𣬲���������ѵ����������˿��������ӣ�Ϊ�ˣ�ij�ж����Dzμ��������˶������������ͳ�Ƶ��飮����һ������ǵ�����Ա�Ӳ����������˶������������ȡ200�ˣ�����ÿ�ܲ��������ɳ���ѵ������������ͳ�ƣ��õ�����ͳ�Ʊ���
ƽ��ÿ�ܽ��г���ѵ������ | ������2�� | 3���4�� | ������5�� |
���� | 30 | 130 | 40 |
��ij��ƽ��ÿ�ܽ��г���ѵ������������5�죬�����Ϊ�����Ҳ����ߡ��������Ϊ�������Ҳ����ߡ���
��1�������飬����Լ��2���˲����������˶����Թ������С����Ҳ����ߡ���������
��2�������ϱ������ݣ���д����2��2����������ͨ�������ж��Ƿ����ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�����Ҳ��������ɡ����Ա��йأ�
���Ҳ����� | �����Ҳ����� | �ϼ� | |
�� | 140 | ||
Ů | 55 | ||
�ϼ� |
����k2=![]() ��n����������
��n����������
P��k2��k0�� | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() :
:![]() �ij��᳤Ϊ4�����Ҷ���ֱ�Ϊ
�ij��᳤Ϊ4�����Ҷ���ֱ�Ϊ![]() ��������
��������![]() �Ķ�ֱ������Բ
�Ķ�ֱ������Բ![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() �������
�������![]() �غϣ�.
�غϣ�.
��1������Բ![]() �ķ��̼������ʣ�
�ķ��̼������ʣ�
��2�����ı���![]() ��������ֵ��
��������ֵ��
��3����ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���жϵ�
���жϵ�![]() �Ƿ�λ��һ����ֱ���ϣ����ǣ�д����ֱ�ߵķ���. �����۲�Ҫ��֤����
�Ƿ�λ��һ����ֱ���ϣ����ǣ�д����ֱ�ߵķ���. �����۲�Ҫ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Բ![]() �����Ҷ���Ϊ
�����Ҷ���Ϊ![]() ��
��![]() ���ϡ��¶���Ϊ
���ϡ��¶���Ϊ![]() ��
��![]() �����ı���
�����ı���![]() ������ԲΪ
������ԲΪ![]() .
.
��1����Բ![]() �ı����̣�
�ı����̣�
��2����֪Բ![]() ��һ������������ƽ�е�����
��һ������������ƽ�е�����![]() ����Բ
����Բ![]() ��P��M����.
��P��M����.
��i����֤��![]() ��
��
��ii����̽��![]() �Ƿ�Ϊ��ֵ.
�Ƿ�Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
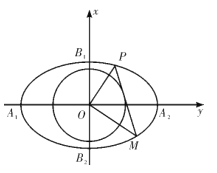
����Ŀ����ͼ����֪Բ![]() ��������
��������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ���ߵķ���Ϊ
���ߵķ���Ϊ![]() ��
��![]() ������
Ϊ������![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ��Բ
��Բ![]() ������������
������������![]() �ύ��
�ύ��![]() .
.

������������![]() �ķ��̣�
�ķ��̣�
������![]() �����
�����![]() ���
���![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com