
【题目】已知椭圆E: ![]() (a>b>0)的上顶点为P(0,1),过E的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆E上,该菱形对角线BD所在直线的斜率为﹣1.
(a>b>0)的上顶点为P(0,1),过E的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆E上,该菱形对角线BD所在直线的斜率为﹣1.
(1)求椭圆E的方程;
(2)当直线BD过点(1,0)时,求直线AC的方程;
(3)当∠ABC= ![]() 时,求菱形ABCD面积的最大值.
时,求菱形ABCD面积的最大值.
【答案】
(1)解:依题意,b=1,
解 ![]() ,得|y|=
,得|y|= ![]() ,
,
所以 ![]() ,a=2,
,a=2,
椭圆E的方程为 ![]()
(2)解:直线BD:y=﹣1×(x﹣1)=﹣x+1,
设AC:y=x+b,
由方程组 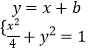 得
得 ![]() ,
,
当 ![]() 时,
时,
A(x1,y1),C(x2,y2)的中点坐标为 ![]() =﹣
=﹣ ![]() ,
, ![]() ,
,
ABCD是菱形,所以AC的中点在BD上,所以 ![]()
解得 ![]() ,满足△=5﹣b2>0,所以AC的方程为y=x﹣
,满足△=5﹣b2>0,所以AC的方程为y=x﹣ ![]()
(3)解:因为四边形ABCD为菱形,且 ![]() ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ![]() ,
,
由(2)可得AC2=(x2﹣x1)2+(y2﹣y2)2=2,
AC2=(x2﹣x1)2+(y2﹣y1)2=2(x2﹣x1)2=2(x2+x1)2﹣8x1x2=2× ![]() =
= ![]() ,
,
因为 ![]() ,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为
,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为 ![]()
【解析】(1)依题意,b=1,解 ![]() ,得|y|=
,得|y|= ![]() ,所以
,所以 ![]() ,由此能求出椭圆E的方程.(2)直线BD:y=﹣1×(x﹣1)=﹣x+1,设AC:y=x+b,由方程组
,由此能求出椭圆E的方程.(2)直线BD:y=﹣1×(x﹣1)=﹣x+1,设AC:y=x+b,由方程组 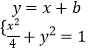 得
得 ![]() ,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.(3)因为四边形ABCD为菱形,且
,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.(3)因为四边形ABCD为菱形,且 ![]() ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ![]() ,由AC2=(x2﹣x1)2+(y2﹣y1)2=2(x2﹣x1)2=2(x2+x1)2﹣8x1x2=
,由AC2=(x2﹣x1)2+(y2﹣y1)2=2(x2﹣x1)2=2(x2+x1)2﹣8x1x2= ![]() ,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.
,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.
【考点精析】根据题目的已知条件,利用一般式方程和椭圆的标准方程的相关知识可以得到问题的答案,需要掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0);椭圆标准方程焦点在x轴:
(A,B不同时为0);椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 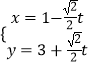 (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2 ![]() sin(θ+
sin(θ+ ![]() ). (Ⅰ)求曲线C1与曲线C2的普通方程;
). (Ⅰ)求曲线C1与曲线C2的普通方程;
(Ⅱ)若点P的坐标为(﹣1,3),且曲线C1与曲线C2交于B,D两点,求|PB||PD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC. (Ⅰ)若a=b,求cosB;
(Ⅱ)设B=90°,且a= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB. 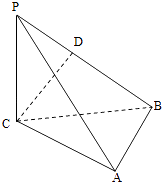
(1)求证:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=2,且anan+1+an+1﹣2an=0(n∈N+).
(1)求a2、a3、a4的值;
(2)猜想数列{an}的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(n)=1+ ![]() +
+ ![]() +…+
+…+ ![]() (n∈N*),计算得f(2)=
(n∈N*),计算得f(2)= ![]() ,f(4)>2,f(8)>
,f(4)>2,f(8)> ![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)> ![]() ,由此推算:当n≥2时,有( )
,由此推算:当n≥2时,有( )
A.f(2n)> ![]() (n∈N*)
(n∈N*)
B.f(2n)> ![]() (n∈N*)
(n∈N*)
C.f(2n)> ![]() (n∈N*)
(n∈N*)
D.f(2n)> ![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0.
(1)求证:直线l恒过定点;
(2)求直线l被圆C截得的弦长最长与最短的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2+4x=0,x∈R},B={x|x2+2(a+1)x+a2﹣1=0,x∈R},
(1)若A∩B=A∪B,求实数a的值;
(2)若A∩B=B,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com