
【题目】设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,直线
,直线![]() 和
和![]() 相交于点
相交于点![]() ,且
,且![]() 和
和![]() 的斜率之差是1.
的斜率之差是1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过轨迹![]() 上的点
上的点![]() ,
,![]() ,作圆
,作圆![]() :
:![]() 的两条切线,分别交
的两条切线,分别交![]() 轴于点
轴于点![]() ,
,![]() .当
.当![]() 的面积最小时,求
的面积最小时,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设出![]() 点坐标,根据
点坐标,根据![]() 和
和![]() 的斜率之差是
的斜率之差是![]() 列方程,化简后求得点
列方程,化简后求得点![]() 的轨迹
的轨迹![]() 的方程.注意排除斜率不存在的情况.
的方程.注意排除斜率不存在的情况.
(2)设出切线的斜率,由点斜式写出切线方程,利用圆心![]() 到切线的距离为
到切线的距离为![]() 列方程,化简后写出关于切线
列方程,化简后写出关于切线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() 的根与系数关系,求得
的根与系数关系,求得![]() 两点的坐标,进而求得
两点的坐标,进而求得![]() 的面积的表达式,化简后利用基本不等式求得
的面积的表达式,化简后利用基本不等式求得![]() 的面积的最小值以及此时对应
的面积的最小值以及此时对应![]() 的值.
的值.
(1)设![]() ,由题意得
,由题意得![]() .
.
化简得点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]() .
.
(2)由点![]() 所引的切线方程必存在斜率,设为
所引的切线方程必存在斜率,设为![]() .
.
则切线方程为![]() ,即
,即![]() .
.
其与![]() 轴的交点为
轴的交点为![]() ,
,
而圆心![]() 到切线的距离
到切线的距离![]() ,
,
整理得:![]() ①,
①,
切线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,则
,则![]() ,
,![]() 是方程①的两根,
是方程①的两根,
故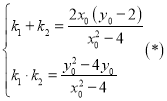 ,
,
而切线与![]() 轴的交点为
轴的交点为![]() ,故
,故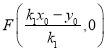 ,
,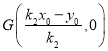 ,
,
又![]() ,
,![]() ,
,
∴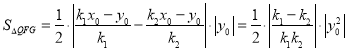
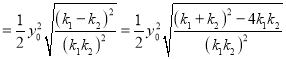 ,
,
将![]() 代入得
代入得
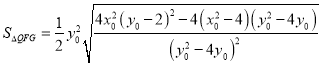
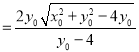 ,
,
而点![]() 在
在![]() 上,故
上,故![]() ,
,
∴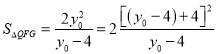
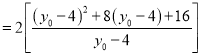
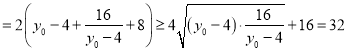 ,
,
当且仅当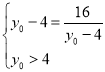 ,即
,即![]() 时等号成立.
时等号成立.
又![]() ,∴
,∴![]() ,
,
故当点![]() 坐标为
坐标为![]() ,
,![]() 时,
时,![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点![]() 满足方程
满足方程![]() .
.
(1)求点M的轨迹C的方程;
(2)作曲线C关于![]() 轴对称的曲线,记为
轴对称的曲线,记为![]() ,在曲线C上任取一点
,在曲线C上任取一点![]() ,过点P作曲线C的切线l,若切线l与曲线
,过点P作曲线C的切线l,若切线l与曲线![]() 交于A,B两点,过点A,B分别作曲线
交于A,B两点,过点A,B分别作曲线![]() 的切线
的切线![]() ,证明
,证明![]() 的交点必在曲线C上.
的交点必在曲线C上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为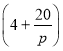 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() ),右焦点
),右焦点![]() ,点
,点![]() 在椭圆上;
在椭圆上;
(1)求椭圆C的标准方程;
(2)是否存在过原点的直线l与椭圆C交于A、B两点,且![]() ?若存在,请求出所有符合要求的直线;若不存在,请说明理由.
?若存在,请求出所有符合要求的直线;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,记
上的函数,记![]() ,
,![]() 的最大值为
的最大值为![]() .若存在
.若存在![]() ,满足
,满足![]()
![]()
![]() ,则称一次函数
,则称一次函数![]() 是
是![]() 的“逼近函数”,此时的
的“逼近函数”,此时的![]() 称为
称为![]() 在
在![]() 上的“逼近确界”.
上的“逼近确界”.
(1)验证:![]() 是
是![]()
![]() 的“逼近函数”;
的“逼近函数”;
(2)已知![]()
![]()
![]()
![]() .若
.若![]() 是
是![]() 的“逼近函数”,求
的“逼近函数”,求![]() 的值;
的值;
(3)已知![]()
![]() 的逼近确界为
的逼近确界为![]() ,求证:对任意常数
,求证:对任意常数![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为内角
分别为内角![]() ,
,![]() ,
,![]() 的对边,且满
的对边,且满![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中,选出两个使
这三个条件中,选出两个使![]() 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求
唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在下图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:

(1)按此规律,n = 5时果树数量及松树数量分别为多少;并写出果树数量![]() ,及松树数量
,及松树数量![]() 关于n的表达式
关于n的表达式
(2)定义:![]()
![]() 为
为![]() 增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com