
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
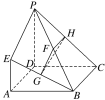
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)通过证明BC⊥平面ABE,FH∥BC,证得FH⊥平面ABE,即可证得面面垂直;
(2)建立空间直角坐标系,利用向量方法求线面角的正弦值.
(1)由题:,AE⊥平面ABCD,BC![]() 平面ABCD,所以AE⊥BC,
平面ABCD,所以AE⊥BC,
四边形ABCD是正方形,AB⊥BC,AE与AB是平面ABE内两条相交直线,
所以BC⊥平面ABE,F,H分别为BP,PC的中点,所以FH∥BC,
所以FH⊥平面ABE,HF![]() 平面GHF,所以平面ABE⊥平面GHF;
平面GHF,所以平面ABE⊥平面GHF;
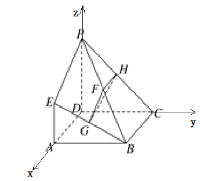
(2)由题可得:DA,DC,DP两两互相垂直,所以以D为原点,DA,DC,DP为x,y,z轴的正方向建立空间直角坐标系如图所示:
![]() ,
,
所以![]() ,设平面PBC的法向量
,设平面PBC的法向量![]() ,
,
 ,取
,取![]() 为平面PBC的一个法向量,
为平面PBC的一个法向量,
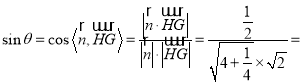
![]()
所以直线GH与平面PBC所成的角θ的正弦值![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,曲线
,曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在第一象限),则
在第一象限),则![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合)已知
是椭圆上一动点(与左、右顶点不重合)已知![]() 的内切圆半径的最大值为
的内切圆半径的最大值为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆C的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解数学课外兴趣小组的学习情况,从某次测试的成绩中随机抽取![]() 名学生的成绩进行分析,得到如图所示的频率分布直方图.
名学生的成绩进行分析,得到如图所示的频率分布直方图.

(1)根据频率分布直方图估计本次测试成绩的众数;
(2)从成绩不低于![]() 分的两组学生中任选
分的两组学生中任选![]() 人,求选出的两人来自同一组的概率.
人,求选出的两人来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.
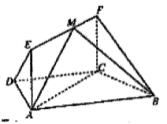
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司组织开展“学习强国”的学习活动,活动第一周甲、乙两个部门员工的学习情况统计如下:
学习活跃的员工人数 | 学习不活跃的员工人数 | |
甲 | 18 | 12 |
乙 | 32 | 8 |
(1)从甲、乙两个部门所有员工中随机抽取1人,求该员工学习活跃的概率;
(2)根据表中数据判断能否有![]() 的把握认为员工学习是否活跃与部门有关;
的把握认为员工学习是否活跃与部门有关;
(3)活动第二周,公司为检查学习情况,从乙部门随机抽取2人,发现这两人学习都不活跃,能否认为乙部门第二周学习的活跃率比第一周降低了?
参考公式: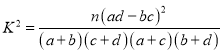 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,(t为参数),直线l与x轴交于点F,与曲线C的交点为A,B,当
,(t为参数),直线l与x轴交于点F,与曲线C的交点为A,B,当![]() 取最小值时,求直线l的直角坐标方程.
取最小值时,求直线l的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com