
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)当![]() 且
且![]() 时,函数
时,函数![]() 的图象总在直线
的图象总在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
![]() 求出函数
求出函数![]() 的导数
的导数![]() ,由切线方程可得
,由切线方程可得![]()
![]() ,解方程即可;
,解方程即可;
![]() 由题意知,
由题意知,![]() 对任意
对任意![]() 恒成立等价于不等式
恒成立等价于不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
令函数![]() ,证明
,证明![]() 在
在![]() 恒成立即可;
恒成立即可;
对函数![]() 进行求导
进行求导![]() ,利用导数
,利用导数![]() 判断函数
判断函数![]() 的单调性,求最值即可求出实数
的单调性,求最值即可求出实数![]() 的取值范围.
的取值范围.
![]() 依题意,
依题意,![]() ,
,
故![]() ,则
,则![]() ,解得
,解得![]() ;
;
![]() 依题意,当
依题意,当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,证明
,证明![]() 在
在![]() 恒成立即可,
恒成立即可,
因为![]() ,
,
令![]() ,当
,当![]() 时,
时,![]() 图象开口向下,
图象开口向下,
又因为![]() 在
在![]() 上有两个零点1和
上有两个零点1和![]() ,
,
①当![]() 时,即
时,即![]() ,此时
,此时![]() 在
在![]() 上恒成立,
上恒成立,
![]() 函数
函数![]() 在
在![]() 上单调递减,因为
上单调递减,因为![]() ,
,
所以函数![]() 在
在![]() 恒成立,符合题意;
恒成立,符合题意;
②当![]() 时,即
时,即![]() ,此时当
,此时当![]() 时,
时, ![]() ,
,
![]() 函数
函数![]() 在
在![]() 上单调递减,因为
上单调递减,因为![]() ,
,
所以函数![]() 在
在![]() 恒成立,符合题意;
恒成立,符合题意;
③当![]() 时,即
时,即![]() ,此时当
,此时当![]() 时,
时,![]() ,
,
当![]() 时,
时, ![]() ,
,
![]() 函数
函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减;
上单调递减;
所以![]() ,不符合题意;
,不符合题意;
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某鲜花店每天制作![]() 、
、![]() 两种鲜花共
两种鲜花共![]() 束,每束鲜花的成本为
束,每束鲜花的成本为![]() 元,售价
元,售价![]() 元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
| 48 | 49 | 50 | 51 |
天数 | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天数 | 40 | 35 | 15 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种鲜花的日销量相互独立.
(1)记该店这两种鲜花每日的总销量为![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鲜花店为了减少浪费,提升利润,决定调查每天制作鲜花的量![]() 束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与
束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-ax-1(e为自然对数的底数),a>0.
(1)若函数f(x)恰有一个零点,证明:aa=ea-1;
(2)若f(x)≥0对任意x∈R恒成立,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
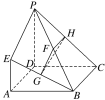
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 在椭圆
在椭圆![]() 上,
上,![]() 为右焦点,
为右焦点,![]() 轴,
轴,![]() 为椭圆上的四个动点,且
为椭圆上的四个动点,且![]() ,
,![]() 交于原点
交于原点![]() .
.
(1)判断直线![]() 与椭圆的位置关系;
与椭圆的位置关系;
(2设![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 的值是否为定值,若是,请求出此定值,并求出四边形
的值是否为定值,若是,请求出此定值,并求出四边形![]() 面积的最大值,否则说明理由.
面积的最大值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二万五千里长征”是1934年10月到1936年10月中国工农红军进行的一次战略转移,是人类历史上的伟大奇迹,向世界展示了中国工农红军的坚强意志,在期间发生了许多可歌可泣的英雄故事.在中国共产党建党![]() 周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生
周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生![]() 名,用分层抽样的方法从该校高中学生中抽取一个容量为
名,用分层抽样的方法从该校高中学生中抽取一个容量为![]() 的样本参加活动,其中高三年级抽了
的样本参加活动,其中高三年级抽了![]() 人,高二年级抽了
人,高二年级抽了![]() 人,则该校高一年级学生人数为( )
人,则该校高一年级学生人数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com